解:(I)∵f(x)=x,
∴g(x)=λx+sinx,
∵g(x)在[-1,1]上单调递减,
∴g'(x)=λ+cosx≤0
∴λ≤-cosx在[-1,1]上恒成立,λ≤-1,故λ的最大值为-1.
(II)由题意[g(x)]
max=g(-1)=-λ-sinl
∴只需-λ-sinl<t
2+λt+1
∴(t+1)λ+t
2+sin+1>0(其中λ≤-1),恒成立,
令h(λ)=(t+1)λ+t
2+sin1+1>0(λ≤-1),
则
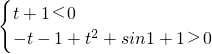
,
∴
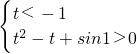
,而t
2-t+sin1>0恒成立,
∴t<-1
又t=-1时-λ-sinl<t
2+λt+1
故t≤-1(9分)
(Ⅲ)由
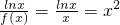
-2ex+m.
令f
1(x)=
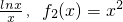
-2ex+m,
∵f
1′(x)=

,
当x∈(0,e)时,f
1′(x)≥0,
∴f
1(x)在(0,e]上为增函数;
当x∈[e,+∞)时,f
1′(x)≤0,
∴f
1(x)在[e,+∞)为减函数;
当x=e时,[f
1(x)]
max=f
1(e)=

,
而f
2(x)=(x-e)
2+m-e
2,
∴当m-e
2>

,即m>
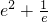
时,方程无解;
当m-e
2=

,即m=
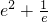
时,方程有一个根;
当m-e
2<

时,m<
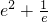
时,方程有两个根.(14分)
分析:(I)由题意由于f(x)=x,所以函数g(x)=λf(x)+sinx=λx+sinx,又因为该函数在区间[-1,1]上的减函数,所以可以得到λ的范围;
(II)由于g(x)<t
2+λt+1在x∈[-1,1]上恒成立?[g(x)]
max=g(-1)=-λ-sinl,解出即可;
(III)利用方程与函数的关系可以构造成两函数图形的交点个数加以分析求解.
点评:此题考查了导函数,利用导函数求解恒成立问题,还考查了方程的根的个数等价于相应的两函数的交点的个数,即函数与方程的解之间的关系.

 的根的个数.
的根的个数.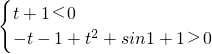 ,
,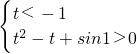 ,而t2-t+sin1>0恒成立,
,而t2-t+sin1>0恒成立,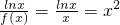 -2ex+m.
-2ex+m.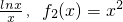 -2ex+m,
-2ex+m, ,
, ,
, ,即m>
,即m>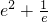 时,方程无解;
时,方程无解; ,即m=
,即m=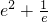 时,方程有一个根;
时,方程有一个根; 时,m<
时,m<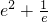 时,方程有两个根.(14分)
时,方程有两个根.(14分)

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<