
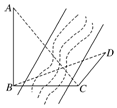
 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | 10米 | B. | 2$\sqrt{6}$米 | C. | $2\sqrt{3}$米 | D. | $3\sqrt{2}$米 |
分析 在△CBD中根据三角形的内角和定理,求出∠CBD=180°-∠BCD-∠BDC=45°,从而利用正弦定理求出BC.然后在Rt△ABC中,根据三角函数的定义加以计算,可得旗杆AB的高度.
解答 解:∵△BCD中,∠BCD=75°,∠BDC=60°,
∴∠CBD=180°-∠BCD-∠BDC=45°,
在△CBD中,CD=2米,根据正弦定理可得BC=$\frac{CD•sin∠BDC}{sin∠CBD}$=$\sqrt{6}$米,
∵Rt△ABC中,∠ACB=60°,
∴AB=BC•tan∠ACB=$\sqrt{6}$•tan60°=3$\sqrt{2}$,即旗杆高,3$\sqrt{2}$米.
故选:D.
点评 本题给出实际应用问题,求棋杆AB的高度.着重考查了三角形内角和定理、利用正弦定理解三角形和三角函数的定义等知识,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 0 | D. | -2或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-2x-6y+9=0 | B. | x2+y2+6x+2y+9=0 | C. | x2+y2-6x-2y+9=0 | D. | x2+y2+2x+6y+9=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[kπ+\frac{3π}{8},kπ+\frac{7π}{8}],k∈Z$ | B. | $[2kπ+\frac{3π}{8},2kπ+\frac{7π}{8}],k∈Z$ | ||
| C. | $[2kπ-\frac{π}{8},2kπ+\frac{3π}{8}],k∈Z$ | D. | $[kπ-\frac{π}{8},kπ+\frac{3π}{8}],k∈Z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
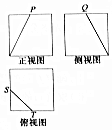 一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )
一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )| A. | 21 | B. | $\frac{43}{2}$ | C. | $\frac{45}{2}$ | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com