
分析 (Ⅰ)确定基本事件的个数,即可求取出2球都是白球的概率;
(Ⅱ)取出两球分数之和为2,包括取1个红球、1个黑球或2个白球,取1个红球、1个黑球的概率为$\frac{1}{6}$,即可求取出两球分数之和为2的概率.
解答 解:(Ⅰ)从袋中取出2球,共有${C}_{4}^{2}$=6种方法,取出2球都是白球,有1种方法,所以取出2球都是白球的概率是${P_1}=\frac{1}{6}$…..(5分)
(Ⅱ)取出两球分数之和为2,包括取1个红球、1个黑球或2个白球,取1个红球、1个黑球的概率均为$\frac{1}{6}$,
∴取出两球分数之和为2的概率${P_2}=\frac{1}{3}$…..(10分)
点评 本题考查古典概型概率的计算,考查互斥事件概率的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
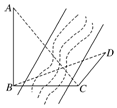 如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )
如图,测量河对岸的旗杆高AB时,选与旗杆底B在同一水平面内的两个测点C与D.测得∠BCD=75°,∠BDC=60°,CD=2米,并在点C测得旗杆顶A的仰角为60°,则旗杆高AB为( )| A. | 10米 | B. | 2$\sqrt{6}$米 | C. | $2\sqrt{3}$米 | D. | $3\sqrt{2}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1358 | B. | 0.1359 | C. | 0.2176 | D. | 0.2718 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.
如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com