
 如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.
如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.分析 (1)设熊猫居室的宽为x,则两间熊猫居室的长为30-3x,进而可得两间熊猫居室的面积y的表达式;
(2)由(1)中所得解析式及自变量x的取值范围,由二次函数的图象和性质,可得函数最大值及最大值点.
解答 (本题满分12分)
解:(1)设熊猫居室的宽为x(单位m),由于可供建造围墙的材料总长是30m
两间熊猫居室的长为30-3x(单位m)…(1分)
所以两间熊猫居室的面积y=x(30-3x)…(3分)
又$\left\{\begin{array}{l}x>0\\ 30-3x>0\end{array}\right.$得0<x<10…(5分)
于是y=-3x2+30x,(0<x<10)为所求…(6分)
(2)又(1)y=-3x2+30x=-3(x-5)2+75二次函数图象开口向下,对称轴x=5…(8分)
且x∈(0,10),当x=5时,所建造的熊猫居室面积最大,…(10分)
使熊猫居室的宽5m,两间居室的长为15m时所建造的熊猫居室面积最大;
其中每间熊猫居室的最大面积为$\frac{75}{2}{m^2}$…(12分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:选择题
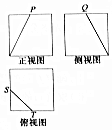 一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )
一个几何体的三视图是如图所示的边长为2的正方形,其中P,Q,S,T为各边的中点,则此几何体的表面积是( )| A. | 21 | B. | $\frac{43}{2}$ | C. | $\frac{45}{2}$ | D. | 23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 我们把离心率e=$\frac{\sqrt{5}+1}{2}$的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)称为黄金双曲线.如图是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,c=$\sqrt{{a}^{2}+{b}^{2}}$)的图象,给出以下几个说法:
我们把离心率e=$\frac{\sqrt{5}+1}{2}$的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)称为黄金双曲线.如图是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,c=$\sqrt{{a}^{2}+{b}^{2}}$)的图象,给出以下几个说法:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com