
分析 (Ⅰ)列出函数的偶函数;定义域R;值域;单调递增区间,单调递减区间,选择3项即可,画出图象.
(Ⅱ)设2x+2-x=t(t≥2),则4x+4-x=t2-2,设k(t)=t2-2-at=t2-at-2,通过a与2讨论,利用二次函数的最值求解即可.
解答 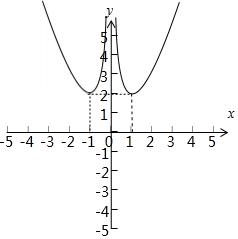 解:(Ⅰ)偶函数;定义域R;值域{y|y≥2};
解:(Ⅰ)偶函数;定义域R;值域{y|y≥2};
单调递增区间:(0,+∞),单调递减区间:(-∞,0)等-----(4分)
图象如图:.-----(6分)
(Ⅱ)设2x+2-x=t(t≥2),则4x+4-x=t2-2,设k(t)=t2-2-at=t2-at-2,
?$\frac{a}{2}≤2,即a≤4$时,k(t)min=k(2)=2-2a;
?$\frac{a}{2}>2,即a>4$时$k{(t)_{min}}=k(\frac{a}{2})=-\frac{a^2}{4}-2$.
所以,?$\frac{a}{2}≤2,即a≤4$时,g(x)min=2-2a;
?$\frac{a}{2}>2,即a>4$时$g{(x)_{min}}=-\frac{a^2}{4}-2$.----(12分)
点评 本题考查函数与方程的应用,二次函数的性质,函数的图象的应用,考查转化思想以及分类讨论思想的应用.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.
如图,动物园要建造一面靠墙的两间相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.
如图,在三棱柱ABC-A1B1C1中,面积为$\frac{9}{2}$的△ACB是等腰直角三角形且∠ACB=90°,C1B⊥面ABC,C1B=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m+a | B. | m-a | C. | m2+a2 | D. | m2-a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com