
分析 设P(cosα,sinα).可得$\overrightarrow{AO}$=(2,0),$\overrightarrow{AP}$=(cosα+2,sinα).利用数量积运算性质、三角函数的单调性与值域即可得出.
解答 解:设P(cosα,sinα).$\overrightarrow{AO}$=(2,0),$\overrightarrow{AP}$=(cosα+2,sinα).
则$\overrightarrow{AO}$•$\overrightarrow{AP}$=2(cosα+2)≤6,当且仅当cosα=1时取等号.
故答案为:6.
点评 本题考查了数量积运算性质、三角函数的单调性与值域、圆的参数方程,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
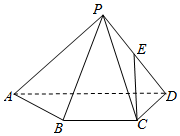 如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
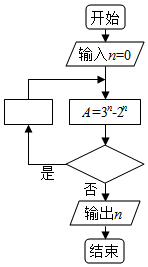 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com