
已知 分别是椭圆
分别是椭圆 的左,右顶点,点
的左,右顶点,点 在椭圆
在椭圆 上,且直线
上,且直线 与直线
与直线 的斜率之积为
的斜率之积为 .
.

(1)求椭圆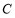 的标准方程;
的标准方程;
(2)点 为椭圆
为椭圆 上除长轴端点外的任一点,直线
上除长轴端点外的任一点,直线 ,
, 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
, .
.
①在 轴上是否存在一个定点
轴上是否存在一个定点 ,使得
,使得 ?若存在,求点
?若存在,求点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②已知常数 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)①存在点
;(2)①存在点 的坐标为
的坐标为 ,②
,② .
.
【解析】
试题分析:(1)利用题目条件建立关于a,b,c的方程组,解方程组即可;
(2)①对于存在性问题,可以先假设点 存在,然后根据
存在,然后根据 以及点P在椭圆上直线
以及点P在椭圆上直线 ,
,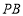 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
, 等相关条件建立方程,看看点E的横坐标是不是定值,如果是即为所求,如果不是也就说明了不存在;②利用向量的坐标运算,计算
等相关条件建立方程,看看点E的横坐标是不是定值,如果是即为所求,如果不是也就说明了不存在;②利用向量的坐标运算,计算 ,
,  ,进而求出
,进而求出 的表达式,在利用函数知识求取值范围.
的表达式,在利用函数知识求取值范围.

试题解析:(1)由题意得, ,
,
 , ∴
, ∴ ,
,
由点 在椭圆C上,则有:
在椭圆C上,则有:
 , 2分
, 2分
由以上两式可解得 .
.
∴椭圆方程为 . 4分
. 4分
(2)①椭圆右准线的方程为 . 5分
. 5分
假设存在一个定点 ,使得
,使得 .设点
.设点
 (
( ).
).
直线 的方程为
的方程为 ,令
,令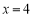 ,
, ,∴点
,∴点 坐标为
坐标为 .
.
直线 的方程为
的方程为 ,令
,令 ,
, ,
,
∴点 坐标为
坐标为 . 7分
. 7分
若 ,则
,则 ,∵
,∵  ,
, ,
,
∴ . 9分
. 9分
∵点 在椭圆
在椭圆 上,∴
上,∴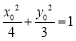 ,∴
,∴ ,代入上式,得
,代入上式,得 ,
,
∴ ,∴点
,∴点 的坐标为
的坐标为 . 11分
. 11分
②∵ ,
,  ,
,
∴ .
.
∵ ,
, ,∴
,∴ .
.
∴
 . 13分
. 13分
设函数 ,定义域为
,定义域为 ,
,
当 时,即
时,即 时,
时, 在
在 上单调递减,
上单调递减, 的取值范围为
的取值范围为 ,
,
当 时,即
时,即 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增, 的取值范围为
的取值范围为 .
.
综上,当 时,
时,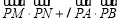 的取值范围为
的取值范围为 ,
,
当 时,
时, 的取值范围为
的取值范围为 . 16分
. 16分
考点:(1)椭圆的标准方程;(2)向量的坐标运算;(3)函数的单调性求值域.


科目:高中数学 来源:2015届江西省宜春市高二上学期期末统考文科数学试卷(解析版) 题型:选择题
各项都是正数的等比数列 的公比
的公比 ,且
,且 成等差数列,则
成等差数列,则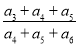 的值为( )
的值为( )
A. B.
B.
C. D.
D. 或
或
查看答案和解析>>
科目:高中数学 来源:2015届江西南昌市四校高二上学期期末联考理科数学试卷(解析版) 题型:选择题
已知

 ,则S1,S2,S3的大小关系为( )
,则S1,S2,S3的大小关系为( )
A. S1<S2<S3 B.S2<S1<S3 C. S2<S3<S1 D.. S3<S2<S1
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试理科数学试卷(解析版) 题型:解答题
已知 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部;  :
: 都有
都有 .
.
(1)若 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若 为假命题,求
为假命题,求 的取值范围;
的取值范围;
(3)若“ 且
且 ”为假命题,且“
”为假命题,且“ 或
或 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试理科数学试卷(解析版) 题型:填空题
已知点P在抛物线 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com