
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:2017届山东枣庄市高三文上学期末期数学试卷(解析版) 题型:选择题
过抛物线 的焦点
的焦点 作斜率为
作斜率为 的直线
的直线 与离心率为
与离心率为 的双曲线
的双曲线 的两条渐近线的交点分别为
的两条渐近线的交点分别为 .若
.若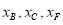 分别表示
分别表示 的横坐标,且
的横坐标,且 ,则
,则 ( )
( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届河北武邑中学高三理周考11.13数学试卷(解析版) 题型:选择题
若在曲线 (或
(或 )上的两个不同点处的切线重合,则称这条切线为曲线
)上的两个不同点处的切线重合,则称这条切线为曲线 (或
(或 )的“自公切线”.下列方程:①
)的“自公切线”.下列方程:① ;②
;② ;③
;③ ;④
;④ 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( )
A.①③ B.①④
C. ②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2017届河北武邑中学高三文上学期调研五数学试卷(解析版) 题型:解答题
已知数列 满足
满足 ,
, 是等差数列,且
是等差数列,且 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2017届河北武邑中学高三文上学期调研五数学试卷(解析版) 题型:选择题
某港口水的深度 是时间
是时间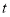 (
( ,单位:
,单位: )的函数,记作
)的函数,记作 .下面是某日水深的数据:
.下面是某日水深的数据:

经长期观察, 的曲线可以近似地看成函数
的曲线可以近似地看成函数 的图象.一般情况下,船舶航行时,船底离海底的距离为
的图象.一般情况下,船舶航行时,船底离海底的距离为 或
或 以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水程度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水程度(船底离水面的距离)为 ,如果该船希望在同一天内安全进出港,请问,它最多能在港内停留( )小时(忽略进出港所需的时间).
,如果该船希望在同一天内安全进出港,请问,它最多能在港内停留( )小时(忽略进出港所需的时间).
A.6 B.12
C.16 D.18
查看答案和解析>>
科目:高中数学 来源:2017届福建福州外国语学校高三文上学期期中数学试卷(解析版) 题型:解答题
已知函数
⑴若函数 在区间[1,2]上是减函数,求实数
在区间[1,2]上是减函数,求实数 的取值范围;
的取值范围;
⑵令 ,是否存在实数
,是否存在实数 ,当
,当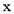 ∈(0,
∈(0, ]时,函数
]时,函数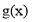 的最小值为3,若存在,求出
的最小值为3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃肃南裕固族自治县一中高三理12月月考数学试卷(解析版) 题型:解答题
某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在 内,发布成绩使用等级制.各等级划分标准见右表,规定:
内,发布成绩使用等级制.各等级划分标准见右表,规定: 三级为合格等级,
三级为合格等级, 为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了
为不合格等级.为了解该校高一年级学生身体素质情况,从中抽取了 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照 ,
, 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示.
(Ⅰ)求 和频率分布直方图中的
和频率分布直方图中的 的值;
的值;
(Ⅱ)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(Ⅲ)在选取的样本中,从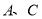 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记 表示所抽取的3名学生中为
表示所抽取的3名学生中为 等级的学生人数,求随机变量
等级的学生人数,求随机变量 的分布列及数学期望.
的分布列及数学期望.


查看答案和解析>>
科目:高中数学 来源:2017届广东汕头市高三理上学期期末数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,以坐标原点为极点,
中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系,半圆
轴正半轴为极轴建立极坐标系,半圆 的极坐标方程为
的极坐标方程为 ,
, .
.
(1)求 的参数方程;
的参数方程;
(2)设点 在
在 上,
上, 在
在 处的切线与直线
处的切线与直线 垂直,根据(1)中你得到的参数方程,确定
垂直,根据(1)中你得到的参数方程,确定 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com