解:(1)由
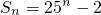
.
当n=1时,a
1=S
1=2×5-2=8,
当n≥2时,
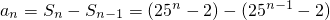
=8•5
n-1.
当n=1时此式成立,
所以
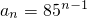
;
(2)由a
n+1=a
n+3n+2.
则a
n+1-a
n=3n+2,a
n-a
n-1=3n-1(n≥2).
又a
1=1,
所以a
n=(a
n-a
n-1)+(a
n-1-a
n-2)+…+(a
2-a
1)+a
1=(3n-1)+[3(n-1)-1]+[3(n-2)-1]+…+(3×2-1)+1
=3(2+3+4+…+n)-(n-1)+1=

=
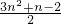
;
(3)由
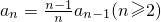
,且a
1=1≠0,
∴
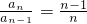
(n≥2),
则
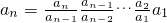
=
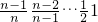
=

;
(4)由a
n+1=3a
n+2,得:a
n+1+1=3(a
n+1),
∵a
1=1,
∴a
1+1=1+1=2≠0,
则
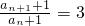
.
所以,数列{a
n+1}是以2为首项,以3为公比的等比数列.
则
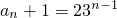
,
所以,
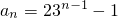
.
分析:(1)在递推式中取n=1可求首项,当n≥2时,由a
n=S
n-S
n-1化简整理可求a
n,然后验证n=1时是否成立,若不成立,则通项公式要分写;
(2)由给出的递推式,采用累加法求数列的通项公式;
(3)根据给出的递推式,可采用累积法求数列的通项公式;
(4)把给出的递推式配方,然后构造出一个新数列{a
n+1},该数列是等比数列,求出a
n+1后即可得到a
n.
点评:本题考查了由数列的前n项和及递推式求数列的通项公式,这是求数列通项公式常见的题型,由前n项和求通项时,一定要注意分类讨论;对于递推式是a
n+1=a
n+f(n)型的,常采用累加法求通项公式;是a
n+1=a
nf(n)型的递推式,常采用累积法,而a
n+1=pa
n+q型的递推式,一定是构造出一个新的等比数列.此题是中档题.

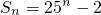 ;
;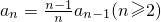 ;
; 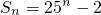 .
.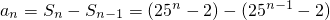 =8•5n-1.
=8•5n-1.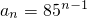 ;
; =
=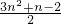 ;
;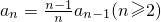 ,且a1=1≠0,
,且a1=1≠0,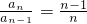 (n≥2),
(n≥2),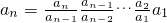 =
=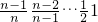 =
= ;
;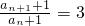 .
.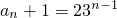 ,
,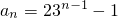 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案