
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 由题意可得F,A,B的坐标,设出直线AE的方程为y=k(x+a),分别令x=-c,x=0,可得M,E的坐标,再由中点坐标公式可得H的坐标,运用三点共线的条件:斜率相等,结合离心率公式,即可得到所求值.
解答 解:由题意可设F(-c,0),A(-a,0),B(a,0),
令x=-c,代入椭圆方程可得y=±$\frac{{b}^{2}}{a}$,可得P(-c,±$\frac{{b}^{2}}{a}$).
设直线AE的方程为y=k(x+a),
令x=-c,可得M(-c,k(a-c)),令x=0,可得E(0,ka),
设OE的中点为H,可得H(0,$\frac{ka}{2}$),由B,H,M三点共线,可得kBH=kBM,即$\frac{a-c}{a+c}=\frac{1}{2}$,即为a=3c,
可得e=$\frac{c}{a}=\frac{1}{3}$.
故选:A.
点评 本题考查椭圆的离心率的求法,注意运用椭圆的方程和性质,以及直线方程的运用和三点共线的条件:斜率相等,考查化简整理的运算能力,属于中档题


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:解答题
 在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.
在某校趣味运动会的颁奖仪式上,为了活跃气氛,大会组委会决定在颁奖过程中进行抽奖活动,用分层抽样的方法从参加颁奖仪式的高一、高二、高三代表队中抽取20人前排就座,其中高二代表队有6人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8,15,7 | B. | 16,2,2 | C. | 16,3,1 | D. | 12,5,3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
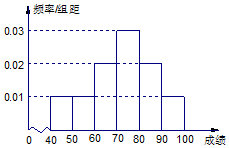 某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).
某校举办安全法规知识竞赛,从参赛的高一学生中抽出100人的成绩作为样本进行统计,并按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分组,得到成绩分布的频率分布直方图(如图).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{11}$ | B. | $\frac{3}{11}$ | C. | $\frac{6}{11}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知长方体ABCD-A1B1C1D1中,AD=AB=2,AA1=1,E为C1D1的中点.
已知长方体ABCD-A1B1C1D1中,AD=AB=2,AA1=1,E为C1D1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com