
分析 (1)根据对数函数的真数大于0,其定义域为R,即可求解k的范围.
(2)由题意y=f(x)=3-x,那么:y=[f(x)]2-2mf(x)+3=3-2x-2m3-x+3存在零点,利用复合函数的单调性讨论其最小值小于等于0,求其m范围;
(3)由题意:h(x)=$\frac{1-mf(-x)}{1+mf(-x)}$=$\frac{1-m{3}^{x}}{1+m{3}^{x}}$=-1+$\frac{2}{1+m{3}^{x}}$(m≠0);函数h(x)在区间[0,1]上讨论m从而确定是否存在上限.
解答 解:(1)由题意:g(x)=log${\;}_{\frac{1}{3}}$x;
那么:g(kx2+2x+1)=log${\;}_{\frac{1}{3}}$(kx2+2x+1)的定义域为R,
则满足:$\left\{\begin{array}{l}{k>0}\\{{b}^{2}-4ac<0}\end{array}\right.$⇒$\left\{\begin{array}{l}{k>0}\\{4-4k<0}\end{array}\right.$,解得:k>1,
故k的范围是(1,+∞).
(2)由题意:g(x)=log${\;}_{\frac{1}{3}}$x的反函数为y=f(x).
那么:f(x)=3-x,
则y=[f(x)]2-2mf(x)+3=(3-x)2-2m3-x+3=(3-x-m)2+3-m2.
∵x∈[-1,1],
∴${3}^{-x}∈[\frac{1}{3},3]$.
当m$≤\frac{1}{3}$时,函数y在区间x∈[-1,1]上是单调减函数,y的最小值为:$(\frac{1}{3}-m)^{2}+3-{m}^{2}$=28-6m.
有零点存在,则:28-6m≤0,解得:$m≥\frac{14}{3}$.
故m的范围是∅.
当m≥3时,函数y在区间x∈[-1,1]上是单调增函数,y的最小值为:(3-m)2+3+m2=12-6m.
有零点存在,则:12-6m≤0,解得:m≥2;
故m的范围是[3,+∞).
当$\frac{1}{3}$<m<3时,y的最小值为:3-m2;
有零点存在,则:3-m2≤0,解得:$m≥\sqrt{3}$或$m≤-\sqrt{3}$;
故m的范围是[$\sqrt{3}$,3).
综上所述:m范围是:[$\sqrt{3}$,+∞).
(3)由题意:h(x)=$\frac{1-mf(-x)}{1+mf(-x)}$=$\frac{1-m{3}^{x}}{1+m{3}^{x}}$=-1+$\frac{2}{1+m{3}^{x}}$(m≠0);
当m>0时,1+m3x>1,则=-1+$\frac{2}{1+m{3}^{x}}$<-1+2=1;
故M≥1;
当m<0时,1+m3x可以趋近于0,
故没有上限.
综上所述:当m>0时,M≥1;
当m<0时,不存在M.
点评 本题考查了对数函数的综合运用能力和计算,分析能力,考查了复合函数的单调性的判断及运用与新定义的结合.属于难题.


科目:高中数学 来源: 题型:填空题
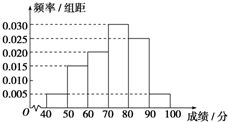 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3-x | B. | f(x)=x2-3x | C. | $f(x)=-\frac{3}{x+2}$ | D. | f(x)=-|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某机构随机抽取50个参与某电视节目的选手的年龄作为样本进行研究,样本数据发组区间为[5,15],[15,25],[25,35],[34,45],[45,55],[55,65]由此得到如图所示的频率分布直方图.
某机构随机抽取50个参与某电视节目的选手的年龄作为样本进行研究,样本数据发组区间为[5,15],[15,25],[25,35],[34,45],[45,55],[55,65]由此得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com