
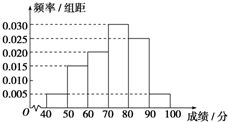
 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 若命题p:?x0∈R,x02-2x0-1>0,则命题¬p:?x∈R,x2-2x-1<0 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10) | B. | (10,20) | C. | (10,15) | D. | (20,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{2}$ | B. | 30 | C. | $-\frac{15}{2}$ | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
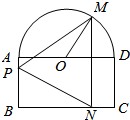 如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值.
如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com