
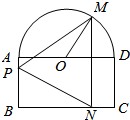
 如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值.
如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值. 分析 设∠MOQ=θ,由θ∈[0,$\frac{π}{2}$],结合锐角三角函数的定义可求MQ=sinθ,OQ=cosθ,代入三角形的面积公式S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$(1+sinθ)(1+cosθ)展开利用换元法,转化为二次函数的最值求解.
解答 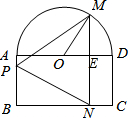 解:设∠MOQ=θ,∴θ∈[0,$\frac{π}{2}$],MQ=sinθ,OQ=cosθ
解:设∠MOQ=θ,∴θ∈[0,$\frac{π}{2}$],MQ=sinθ,OQ=cosθ
∴S△PMN=$\frac{1}{2}$MN•AQ=$\frac{1}{2}$(1+sinθ)(1+cosθ)
=$\frac{1}{2}$(1+sinθcosθ+sinθ+cosθ)….(6分)
令sinθ+cosθ=t∈[1,$\sqrt{2}$],
∴S△PMN=$\frac{1}{2}$(t+1+$\frac{{t}^{2}-1}{2}$)
θ=$\frac{π}{4}$,当t=$\sqrt{2}$,
∴S△PMN的最大值为$\frac{3+2\sqrt{2}}{4}$.…(11分)
点评 本题主要考查了三角函数的定义的应用及利用三角函数求解函数的最值,换元法的应用是求解的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
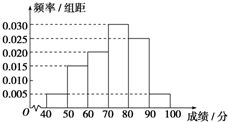 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3-x | B. | f(x)=x2-3x | C. | $f(x)=-\frac{3}{x+2}$ | D. | f(x)=-|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-3,+∞) | C. | [-5,-2] | D. | (-5,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某机构随机抽取50个参与某电视节目的选手的年龄作为样本进行研究,样本数据发组区间为[5,15],[15,25],[25,35],[34,45],[45,55],[55,65]由此得到如图所示的频率分布直方图.
某机构随机抽取50个参与某电视节目的选手的年龄作为样本进行研究,样本数据发组区间为[5,15],[15,25],[25,35],[34,45],[45,55],[55,65]由此得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex1-ex2<lnx1-lnx2 | B. | ex1-ex2>lnx1-lnx2 | ||
| C. | x1ex2<x2ex1 | D. | x1ex2>x2ex1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com