
分析 (1)由等差数列的性质S5=5a3=15,求得a3=3,由d=a3-a2=1,an=a2+(n-2)d=n,根据等差数列前n项和公式即可求得Sn;
(2)$\frac{{{b_{n+1}}}}{b_n}=\frac{1}{2}•\frac{n+1}{n}$,采用“累乘法”即可求得${b_n}=\frac{n}{2^n}$,“错位相减法”即可求得前n项和为Tn;
(3)由集合A可知:A=$\{n|\frac{{2{S_n}(2-{T_n})}}{n+2}≥λ,n∈{N^*}\}$,令$f(n)=\frac{{{n^2}+n}}{2^n}$,利用函数的单调性建立不等进行求解,实数λ的取值范围.
解答 解:(1)由等差数列性质可知,S5=5a3=15,即a3=3,由d=a3-a2=1,
∴an=a2+(n-2)d=n,…(2分)
∴${S_n}=\frac{{{n^2}+n}}{2}$.…(4分)
(2)由$\frac{{{b_{n+1}}}}{b_n}=\frac{1}{2}•\frac{n+1}{n}$得$\frac{b_2}{b_1}=\frac{1}{2}•\frac{2}{1},\frac{b_3}{b_2}=\frac{1}{2}•\frac{3}{2},\frac{b_4}{b_3}=\frac{1}{2}•\frac{4}{3},…,\frac{b_n}{{{b_{n-1}}}}=\frac{1}{2}•\frac{n}{n-1}$,
∴当n≥2时,$\frac{b_n}{b_1}={(\frac{1}{2})^{n-1}}n$,即${b_n}=\frac{n}{2^n}$,
当n=1时,${b_1}=\frac{1}{2}$,适合上式,
∴${b_n}=\frac{n}{2^n}$.…(6分)
${T_n}=\frac{1}{2^1}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}$,
①$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{n-1}{2^n}+\frac{n}{{{2^{n+1}}}}$,②
①-②得,$\frac{1}{2}{T_n}=\frac{1}{2^1}+\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+…+\frac{1}{2^n}-\frac{n}{{{2^{n+1}}}}=\frac{{\frac{1}{2}(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}-\frac{n}{{{2^{n+1}}}}=1-\frac{n+2}{{{2^{n+1}}}}$,
∴${T_n}=2-\frac{n+2}{2^n}$.…(10分)
(3)∵$A=\{n|2{S_n}(2-{T_n})≥λ(n+2),n∈{N^*}\}$=$\{n|\frac{{2{S_n}(2-{T_n})}}{n+2}≥λ,n∈{N^*}\}$…(11分)
由上面得$\frac{{2{S_n}(2-{T_n})}}{n+2}=\frac{{{n^2}+n}}{2^n}$,令$f(n)=\frac{{{n^2}+n}}{2^n}$,
∵$f(n+1)-f(n)=\frac{{{{(n+1)}^2}+n+1}}{{{2^{n+1}}}}-\frac{{{n^2}+n}}{2^n}=\frac{(n+1)(2-n)}{{{2^{n+1}}}}$,
∴当n≥3时,f(n+1)-f(n)<0,即f(n+1)<f(n)…(12分)
又f(1)=1,$f(\frac{3}{2})=\frac{3}{2}$,$f(3)=\frac{3}{2}$,$f(4)=\frac{5}{4}$,$f(5)=\frac{15}{16}$,$f(6)=\frac{21}{32}$…(14分)
∵集合A中有且仅有5个元素,
∴$\frac{{{n^2}+n}}{2^n}≥λ$,n∈N*解的个数为5,
∴$\frac{21}{32}<λ≤\frac{15}{16}$.…(16分)
点评 本题考查等差数列的性质,等差数列前n项和公式,考查“累乘法”及“错位相减法”的应用,考查数列与不等式相结合,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD上的点,且AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD上的点,且AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
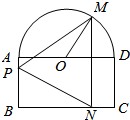 如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值.
如图,一个由半圆和长方形组成的铁皮,已知长方形的边AD为半圆的直径,O为半圆的圆心,AB=1,BC=2,现要将此铁皮剪成一个等腰三角形PMN,且底边MN⊥BC,求剪下的铁皮△PMN的面积的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p∧q | B. | p∧q | C. | p∨¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | ||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com