
分析 根据所给的分段函数,当x小于等于0和x大于0两种情况,根据分段函数分别得到f(x)的解析式,把得到的f(x)的解析式分别代入不等式得到两个不等式,分别求出解集,求出两解集的并集即可得到原不等式的解集.
解答 解:当x>0时,f(x)=2x,代入不等式得:2x<x+2,
解得x<2,所以原不等式的解集为(0,2);
当x≤0时,f(x)=x2,代入不等式得:x2<x+2
解得-1<x<2,所以原不等式的解集为(-1,0],
综上原不等式的解集为(-1,2).
故答案为:(-1,2).
点评 本题考查了不等式的解法及分段函数,考查分类讨论的思想,本题解题的关键是对于求出的范围一定要和分段函数的范围分别并起来,是一个基础题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
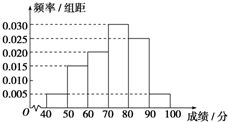 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3-x | B. | f(x)=x2-3x | C. | $f(x)=-\frac{3}{x+2}$ | D. | f(x)=-|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com