
分析 (I)由椭圆的定义可知,抛物线的焦点($\frac{p}{2}$,0),根据抛物线上的点到直线l1和直线l2的距离之和的最小值为焦点F到直线l2的距离,根据点到直线的距离公式,即可求得p的值,求得抛物线方程;
(II)设直线M(x0,y0),y-y0=k(x-x0),代入抛物线方程,由与抛物线相切,△=0,求得k=$\frac{2}{{y}_{0}}$,代入求得N点坐标,求得向量$\overrightarrow{OM}$和$\overrightarrow{QN}$,$\overrightarrow{OM}$•$\overrightarrow{QN}$=0,根据向量数量积的坐标运算,(1-x1)x0+${x}_{1}^{2}$+x1-2=0,即可求得x1=1,即在x轴上存在点到Q(1,0)在以MN为直径的圆上.
解答 解:(I)由题意可知,l2为抛物线的准线,抛物线的焦点坐标为($\frac{p}{2}$,0),
由抛物线的定义可知抛物线上的点到直线l2的距离等于其到焦点F的距离,
∴抛物线上的点到直线l1和直线l2的距离之和的最小值为焦点F到直线l2的距离,
∴d=$\frac{丨2p+6丨}{\sqrt{{3}^{2}+{4}^{2}}}$=2,解得:p=2,
∴抛物线的方程为:y2=4x,
(II)设M(x0,y0),由题意可知,直线l的斜率存在且不等于0,设为直线的斜率为k,
则直线方程为:y-y0=k(x-x0),代入抛物线线方程,整理得:ky2-4y+4y0-k${y}_{0}^{2}$=0,
△=16-4k(4y0-k${y}_{0}^{2}$)=0,求得k=$\frac{2}{{y}_{0}}$,
∴直线l的方程为:y-y0=$\frac{2}{{y}_{0}}$(x-x0),令x=-1,又由${y}_{0}^{2}=4{x}_{0}$,可知N(-1,$\frac{{y}_{0}^{2}-4}{2{y}_{0}}$),
设Q(x1,0),$\overrightarrow{OM}$=(x0-x1,y0),$\overrightarrow{QN}$=(-1-x1,$\frac{{y}_{0}^{2}-4}{2{y}_{0}}$),
由题意可知$\overrightarrow{OM}$•$\overrightarrow{QN}$=0,
∴(x0-x1)(-1-x1)+y0•$\frac{{y}_{0}^{2}-4}{2{y}_{0}}$=0,
把${y}_{0}^{2}=4{x}_{0}$,代入上式,可得:(1-x1)x0+${x}_{1}^{2}$+x1-2=0,
∵对任意的x0等式恒成立,$\left\{\begin{array}{l}{1-{x}_{1}=0}\\{{x}_{1}^{2}+{x}_{1}-2=0}\end{array}\right.$,
∴x1=1,即在x轴上存在点到Q(1,0)在以MN为直径的圆上.
点评 本题考查抛物线的方程及性质,考查直线与抛物线的位置关系,抛物线的定义,向量数量积的坐标运算的综合应用,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
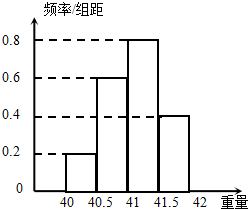 某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )
某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )| A. | 160件 | B. | 120件 | C. | 80件 | D. | 60件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3,1 | B. | 2,2 | C. | 2,1 | D. | 1,3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{3}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) | |
| B. | 向右平移$\frac{π}{6}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| C. | 向左平移$\frac{π}{3}$个单位,再把各点的纵坐标缩短到原来的3倍(横坐标不变) | |
| D. | 向左平移$\frac{π}{6}$个单位,再把各点的纵坐标伸长到原来的3倍(横坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log23 | B. | log23或-1 | C. | log23或0 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com