
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
分析 利用向量的模的平方,求出xy的关系式,化简所求的表达式求解即可.
解答 解:平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是60°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,|x$\overrightarrow{a}$+y$\overrightarrow{b}$|=$\sqrt{3}$(x,y∈R),
可得x2${\overrightarrow{a}}^{2}$+y2${\overrightarrow{b}}^{2}$+2xy$\overrightarrow{a}•\overrightarrow{b}$=3,
x2+y2+xy=3,
3≥2|xy|+xy,当xy同号时,0<xy≤1,当xy异号时,-3≤xy<0.-xy≤3.
|x$\overrightarrow{a}$-y$\overrightarrow{b}$|2=x2${\overrightarrow{a}}^{2}$+y2${\overrightarrow{b}}^{2}$-2xy$\overrightarrow{a}•\overrightarrow{b}$=x2+y2-2xy=3-2xy≤9,此时xy异号.并且|x|=|y|时成立.
则|x$\overrightarrow{a}$-y$\overrightarrow{b}$|的最大值是3.
故选:C.
点评 本题考查向量在几何中的应用,向量的模的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,DF⊥AB于点F,且AE=8,AB=10.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,DF⊥AB于点F,且AE=8,AB=10.| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
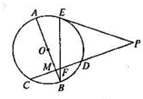 如图所示,AB是圆O的直径,PC是圆O的一条割线,且交圆O于C、D两点,AB⊥PC,PE是圆O的一条切线,切点为E,AB与BE分别交PC于M、F两点.
如图所示,AB是圆O的直径,PC是圆O的一条割线,且交圆O于C、D两点,AB⊥PC,PE是圆O的一条切线,切点为E,AB与BE分别交PC于M、F两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com