
分析 先根据ρcosθ=x,ρsinθ=y,ρ2=x2+y2将点A的极坐标化为直角坐标为(2,-2),圆E的极坐标方程化为直角坐标方程为(x-2)2+(y-2)2=8,再根据点A到圆心距离d与半径比较,即可得出点A与圆E的位置关系.
解答 解:点A的极坐标为$({2\sqrt{2},-\frac{π}{4}})$化为:点A的直角坐标为(2,-2),
圆E的直角坐标方程为(x-2)2+(y-2)2=8,
则点A到圆心E的距离$d=\sqrt{{{(2-2)}^2}+{{(-2-2)}^2}}=4>r=2\sqrt{2}$,
所以点A在圆E外.
点评 本题考查了极坐标方程与直角坐标方程的互化、两点之间距离公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
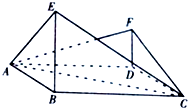 如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.
如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 贵阳市某中学高三(2)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162,170,171,182,163,158,179,168,183,168,篮球队10人的身高(单位:cm)分别是:170,159,162,173,181,165,176,168,178,179.
贵阳市某中学高三(2)班排球队和篮球队各有10名同学,现测得排球队10人的身高(单位:cm)分别是:162,170,171,182,163,158,179,168,183,168,篮球队10人的身高(单位:cm)分别是:170,159,162,173,181,165,176,168,178,179.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
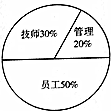 已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )
已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )| A. | 40 | B. | 20 | C. | 12 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com