
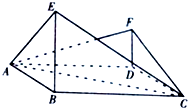
 如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.
如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.分析 (Ⅰ)连结BD,设BD∩AC=G.由已知证得△BAD≌△BCD,得AG=CG,再由线面垂直的判定证明AC⊥平面EBDF,以G为坐标原点,分别以$\overrightarrow{GB}、\overrightarrow{GC}$的方向为x轴,y轴正方向,建立空间直角坐标系G-xyz,设出BE,结合$\overrightarrow{AE}•\overrightarrow{CF}=0$求得BE;
(Ⅱ)由(Ⅰ)可知∠EGF是二面角E-AC-F的平面角,然后利用余弦定理求得使二面角E-AC-F的大小是60°时的BE.
解答 解:(Ⅰ)连结BD,设BD∩AC=G.
由已知得△BAD≌△BCD,∴AG=CG,
∴G为AC的中点,则BD⊥AC,BE⊥AC,且BD∩BE=B,
∴AC⊥平面EBDF,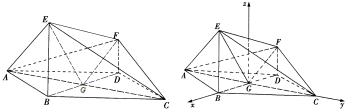
如图,以G为坐标原点,分别以$\overrightarrow{GB}、\overrightarrow{GC}$的方向为x轴,y轴正方向,建立空间直角坐标系G-xyz,
令BE=x,由已知可得B($\sqrt{3}$,0,0),A(0,-1,0),E($\sqrt{3}$,0,x),F(-1,0,1),C(0,1,0),
∴$\overrightarrow{AE}=(\sqrt{3},1,x)$,$\overrightarrow{CF}=(-1,-1,1)$,
由$\overrightarrow{AE}•\overrightarrow{CF}=0$得,x=1+$\sqrt{3}$;
(Ⅱ)由(Ⅰ)可知∠EGF是二面角E-AC-F的平面角,即∠EGF=60°,
则$EG=\sqrt{{x}^{2}+3}$,FG=$\sqrt{2}$,EF=$\sqrt{{x}^{2}-2x+5+2\sqrt{3}}$,
∴cos∠EGF=$\frac{E{G}^{2}+F{G}^{2}-E{F}^{2}}{2EG•GF}=\frac{1}{2}$,解得$x=2\sqrt{3}+3$.
点评 本题考查二面角的平面角的求法,考查空间向量在求解空间几何体中的应用,是中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com