
分析 (Ⅰ)当1<x<2时,x-1>0,欲使f(x)>1恒成立,即$\frac{x-1}{{lnx-m{x^2}}}$>1恒成立,只要满足$\left\{\begin{array}{l}{lnx-m{x}^{2}>0}\\{x-1>lnx-m{x}^{2}}\end{array}\right.$对x∈(1,2)恒成立即可,分别构造辅助函数,求导,根据函数的单调性,求得m的取值范围;
(Ⅱ)采用数学归纳法,当n=1时,a1=$\sqrt{e}$,2lna1=2ln$\sqrt{e}$=1,当n=1时命题成立,假设n=k时命题成立,要证明n=k+1时命题成立,即证明2k+1lnak+1≥1,只需证明ak+1≥e-2(k+1),构造辅助函数求导,根据函数的单调性,即可求证f(${e}^{{2}^{-k}}$)=$\frac{{e}^{{2}^{-k}}-1}{{2}^{-k}}$>${e}^{{2}^{-(k+1)}}$,f(${e}^{{2}^{-k}}$)=$\frac{{e}^{{2}^{-k}}-1}{{2}^{-k}}$>${e}^{{2}^{-(k+1)}}$.
解答 解:(Ⅰ)当1<x<2时,x-1>0,欲使f(x)>1恒成立,即$\frac{x-1}{{lnx-m{x^2}}}$>1恒成立,
只要满足$\left\{\begin{array}{l}{lnx-m{x}^{2}>0}\\{x-1>lnx-m{x}^{2}}\end{array}\right.$对x∈(1,2)恒成立即可.…(2分)
对于lnx-mx2>0,即m<$\frac{lnx}{{x}^{2}}$,
令h(x)=$\frac{lnx}{{x}^{2}}$,则h′(x)=$\frac{1-2lnx}{{x}^{3}}$,
∴函数h(x)在(1,$\sqrt{e}$)内单调递增,在($\sqrt{e}$,2)内单调递减,
而h(1)=0<h(2)=$\frac{ln2}{4}$,
∴m≤0.…(3分)
对于x-1>lnx-mx2,即m>$\frac{lnx-x+1}{{x}^{2}}$,令φ(x)=$\frac{lnx-x+1}{{x}^{2}}$,
则φ′(x)=$\frac{(\frac{1}{x}-1)•{x}^{2}-2x(lnx-x+1)}{{x}^{4}}$=$\frac{x-1-2lnx}{{x}^{3}}$,
令g(x)=x-1-2lnx则g′(x)=$\frac{x-2}{x}$<0,
∴g(x)=x-1-2lnx在(1,2)内单调递减,则x-1-2lnx<0,从而φ′(x)<0,
∴φ(x)在(1,2)内单调递减,则φ(x)<0且当x→1时,φ(x)→x,
∴m≥0,
综上所述可得:m=0.…(6分)
(Ⅱ)下面用数学归纳法证明2nlnan≥1,
(1)当n=1时,a1=$\sqrt{e}$,
∴2lna1=2ln$\sqrt{e}$=1,
∴当n=1时命题成立.…(7分)
(2)假设n=k时命题成立,即2nlnan≥1,要证明n=k+1时命题成立,即证明2k+1lnak+1≥1.
只需证明ak+1≥e-2(k+1),
∵ak+1=f(ak)即证明f(ak)≥e-2(k+1),
由f′(x)=($\frac{x-1}{lnx}$)′=$\frac{lnx+\frac{1}{x}-1}{(lnx)^{2}}$,
当x>1时,易证lnx+$\frac{1}{x}$-1>0,
∴f′(x)>0,函数f(x)在区间(1,+∞)上为增函数.
由归纳假设2klnak+1≥1,得ak≥${e}^{{2}^{-k}}$>1,
∴f(ak)>f(${e}^{{2}^{-k}}$)=$\frac{{e}^{{2}^{-k}}-1}{ln{e}^{{2}^{-k}}}$=$\frac{{e}^{{2}^{-k}}-1}{{2}^{-k}}$,?
若f(${e}^{{2}^{-k}}$)≥${e}^{{2}^{-(k+1)}}$,则必有f(ak)≥${e}^{{2}^{-(k+1)}}$,故现在证明f(${e}^{{2}^{-k}}$)≥${e}^{{2}^{-(k+1)}}$…(9分)
构造函数u(x)=ex-x${e}^{\frac{x}{2}}$-1,则u′(x)=ex-${e}^{\frac{x}{2}}$-$\frac{x}{2}$${e}^{\frac{x}{2}}$=${e}^{\frac{x}{2}}$(${e}^{\frac{x}{2}}$-$\frac{x}{2}$-1),
∵x>0,易证${e}^{\frac{x}{2}}$-$\frac{x}{2}$-1>0,u′(x)>0,
∴函数u(x)在(0,+∞)上为增函数,
故u($\frac{1}{{2}^{k}}$)>u(0)=0,即${e}^{\frac{1}{{2}^{k}}}$-$\frac{1}{{2}^{k}}$•${e}^{\frac{1}{2}•\frac{1}{{2}^{k}}}$-1>0,
则f(${e}^{{2}^{-k}}$)=$\frac{{e}^{{2}^{-k}}-1}{{2}^{-k}}$>${e}^{{2}^{-(k+1)}}$,
由(1)及题意知f(${e}^{{2}^{-k}}$)=$\frac{{e}^{{2}^{-k}}-1}{{2}^{-k}}$>${e}^{{2}^{-(k+1)}}$,
综合(1)(2)知:对任意的n∈N*都有2nlnan≥1成立.…(12分)
点评 本题考查利用导数求函数的单调性及极值的综合运用,考查数学归纳法求证不等式成立,构造法求函数的单调性,考查学生的归纳推理能力,属于难题.


科目:高中数学 来源: 题型:解答题
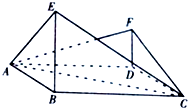 如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.
如图,在四边形ABCD中,△ABC是边长为2的等边三角形,AD丄DC,AD=DC,E、F是平面ABCD同一侧的两点,BE丄平面ABCD,DF丄平面ABCD,且DF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-4=0 | B. | x-y=0 | C. | 2x-y-2=0 | D. | 2x+y-6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
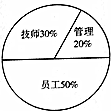 已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )
已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )| A. | 40 | B. | 20 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com