
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
分析 (1)首先求出x,y的平均数,利用最小二乘法做出b的值,再利用样本中心点满足线性回归方程和前面做出的横标和纵标的平均值,求出a的值,写出线性回归方程.
(2)第6名推销员的工作年限为11年,即当x=11时,把自变量的值代入线性回归方程,得到y的预报值,即估计出第6名推销员的年推销金额为5.9万元.
解答 解:(1)设所求的线性回归方程为 $\widehaty=\widehatbx+\widehata,\overline x=6,\overline y=3.4$,…(4分)
则$\widehatb=\frac{{\sum_{i=1}^5{{x_i}{y_i}-5\overline x\overline y}}}{{\sum_{i=1}^5{x_i^2-5{{\overline x}^2}}}}=\frac{112-5×6×3.4}{{200-5×{6^2}}}=0.5$,$\widehata=\overline y-\widehatb\overline x=0.4$.…(7分)
所以年推销金额y关于工作年限x的线性回归归方程为$\widehaty=0.5x+0.4$.…(8分)
(2)当x=11时,y=0.5x+0.4=0.5×11+0.4=5.9(万元).
所以可以估计第6名推销员的年推销金额为5.9万元.
点评 本题考查回归分析的初步应用,考查利用最小二乘法求线性回归方程,是一个综合题目.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
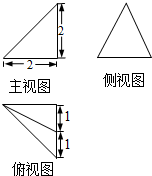
| A. | $\frac{{41\sqrt{41}π}}{48}$ | B. | 12π | C. | $\frac{25π}{4}$ | D. | $\frac{41π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com