
分析 (1)优先安排甲,其他任意排.问题得以解决;
(2)利用除法即可求出女生乙不能站在女生丙的左边的站法;
(3)特殊元素特殊对待,分两类,若乙在正中间,若乙不站在正中间,根据分类计数原理可得.
解答 解:(1)男生甲必须站在两端,其余的进行全排列即可,故有A21A66=1440种;
(2)女生乙不能站在女生丙的左边,有A77÷A22=2520 种;
(3)分两类,若乙在正中间,则有A66=720种,
若乙不站在正中间,乙不站在两端,则乙从另外4个位置任选一个,丙从另外5个位置选一个,其他任意排,故有A41A51A55=2400种,
根据分类计数原理得共有720+2400=3120种.
点评 本题主要考查了排列再实际问题中的应用,考查了相邻问题,顺序确定问题,有限制元素的问题的解法,做题过程中注意总结题型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
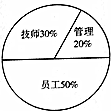 已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )
已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )| A. | 40 | B. | 20 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x,y∈R,若x≠0或y≠0,则xy≠0 | B. | ?x,y∈R,若x≠0且y≠0,则xy≠0 | ||
| C. | ?x,y∈R,若x≠0或y≠0,则xy≠0 | D. | ?x,y∈R,若x≠0且y≠0,则xy≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com