
分析 (Ⅰ)首先利用三角函数的关系式的恒等变换把函数的关系式变性成正弦型函数,进一步求出函数的周期和最值.
(Ⅱ)利用函数的关系式,首先根据三角形的交的他范围,进一步求出C的大小,最后利用正弦和余弦定理求出结果.
解答 解:(Ⅰ)f(x)=$\frac{\sqrt{3}}{2}$sin2x-cos2x-$\frac{1}{2}$,
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1+cos2x}{2}$-$\frac{1}{2}$,
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x-1,
=sin(2x-$\frac{π}{6}$)-1.
∴f(x)的最小正周期是$T=\frac{2π}{2}=π$.
∵0<x<$\frac{π}{2}$,则$f(x)∈(-\frac{3}{2},0]$;
(Ⅱ)由$f(C)=sin(2C-\frac{π}{6})-1=0$,得到$sin(2C-\frac{π}{6})=1$,
∴$2C-\frac{π}{6}=\frac{π}{2}$,即$C=\frac{π}{3}$,
∵sinB=2sinA,
∴由正弦定理得b=2a①,
又$c=\sqrt{3}$,
∴由余弦定理,得${{c}^{2}}={{a}^{2}}+{{b}^{2}}-2abcos\frac{π}{3}$,即a2+b2-ab②,
联立①②解得:$\left\{\begin{array}{l}{a=2}\\{b=4}\end{array}\right.$.
点评 本题考查了倍角公式、和差公式三角函数的周期公式、正弦函数的单调性,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
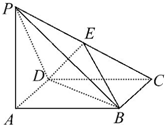 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点.
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
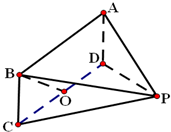 如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PAB是正三角形,且平面ABCD⊥平面PCD.
如图,已知四边形ABCD是矩形,AB=2BC=2,三角形PAB是正三角形,且平面ABCD⊥平面PCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com