
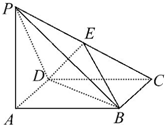
 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点.
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点.分析 (1)连接AC交BD于点O,连接OE,由中位线定理得出PA∥OE,故结论成立;
(2)VE-ABCD=$\frac{1}{2}$VP-ABCD,代入体积公式计算即可.
解答  证明:(1)连接AC交BD于点O,连接OE.
证明:(1)连接AC交BD于点O,连接OE.
∵四边形ABCD是菱形,
∴O为AC的中点,又E为PC的中点,
∴EO∥PA.
∵PA?平面BDE,EO?平面BDE,
∴PA∥平面BDE.
(2)S菱形ABCD=$\frac{1}{2}AC•BD$=12,
VP-ABCD=$\frac{1}{3}$S菱形ABCD•PA=$\frac{1}{3}×12×3$=12.
∵E为PC的中点,
∴VE-ABCD=$\frac{1}{2}$VP-ABCD=6.
点评 本题考查了线面平行的判定,棱锥的体积计算,属于中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
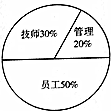 已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )
已知某企业工作人员的配置以及比例如图所示,为了调查各类工作人员的薪资状况,现利用分层抽样的方法抽取部分工作人员进行薪资调查,若抽取的管理人员有8人,则抽取的技师人数为( )| A. | 40 | B. | 20 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x,y∈R,若x≠0或y≠0,则xy≠0 | B. | ?x,y∈R,若x≠0且y≠0,则xy≠0 | ||
| C. | ?x,y∈R,若x≠0或y≠0,则xy≠0 | D. | ?x,y∈R,若x≠0且y≠0,则xy≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20≤x≤30 | B. | 20≤x≤45 | C. | 15≤x≤30 | D. | 15≤x≤45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1]∪[1,2] | B. | [-2,-1]∪[0,1] | C. | [-2,0]∪[1,2] | D. | [-1,0]∪[1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com