
 ������ij��ѧ������2��������Ӻ�����Ӹ���10��ͬѧ���ֲ�������10�˵����ߣ���λ��cm���ֱ��ǣ�162��170��171��182��163��158��179��168��183��168�������10�˵����ߣ���λ��cm���ֱ��ǣ�170��159��162��173��181��165��176��168��178��179��
������ij��ѧ������2��������Ӻ�����Ӹ���10��ͬѧ���ֲ�������10�˵����ߣ���λ��cm���ֱ��ǣ�162��170��171��182��163��158��179��168��183��168�������10�˵����ߣ���λ��cm���ֱ��ǣ�170��159��162��173��181��165��176��168��178��179������ ��1���Ȼ�����Ҷͼ�磬�ɴ�����������ӵ����ߵ�ƽ������
��2�������������߳���178cm��ѧ������5�ˣ�����3����������Ӽ�Ϊa��b��c��2����������Ӽ�ΪA��B�������оٷ������ǡ���������������һ����������ӵĸ��ʣ�
��� ����С������12�֣�
�⣺��1��������Ҷͼ��ͼ��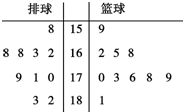
��2�֣�${\overline x_{����}}=170.4$����4�֣�${\overline x_{����}}=171.1$����6�֣�
��2�������������߳���178cm��ѧ������5�ˣ�
����3����������Ӽ�Ϊa��b��c��2����������Ӽ�ΪA��B��
���5���г�ȡ3��ѧ���Ļ����¼�Ϊ��
{a��b��c}��{a��b��A}��{a��b��B}��{a��c��A}��{a��c��B}��
{a��A��B}��{b��c��A}��{b��c��B}��{b��A��B}��{c��A��B}����10����
����ǡ��2�����������1����������ӵ��¼�Ϊ��
{a��b��A}��{a��b��B}��{a��c��A}��{a��c��B}��
{b��c��A}��{b��c��B}����6����
��ǡ��2�����������1����������ӵĸ���$P=\frac{3}{5}$����12�֣�
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O�ڵ�D��DE��AC����AC���ӳ����ڵ�E��DF��AB�ڵ�F����AE=8��AB=10��
��ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O�ڵ�D��DE��AC����AC���ӳ����ڵ�E��DF��AB�ڵ�F����AE=8��AB=10��| A�� | �٢ڢ� | B�� | �ڢۢ� | C�� | �٢ۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x1��x2��R��x1��x2��$x_1^3��x_2^3$ | B�� | ?x1��x2��R��x1��x2��$x_1^3��x_2^3$ | ||
| C�� | ?x1��x2��R��x1��x2��$x_1^3��x_2^3$ | D�� | ?x1��x2��R��x1��x2��$x_1^3��x_2^3$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
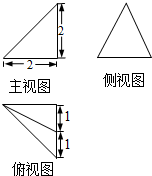
| A�� | $\frac{{41\sqrt{41}��}}{48}$ | B�� | 12�� | C�� | $\frac{25��}{4}$ | D�� | $\frac{41��}{4}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com