
分析 (1)确定符合条件的课代表人员的选法,再进行全排,即可得出结论;
(2)除去该女生后,即相当于挑选剩余的5名学生担任两科的课代表,利用排列可得结论;
(3)从剩余的5名学生中选出2名有$C_5^2$种选法,排列方法有$C_2^1A_2^2$种,利用乘法原理得出结论.
解答 解:(1)符合条件的课代表人员的选法有$(C_2^1C_4^2+C_2^2C_4^1)$种,排列方法有$A_3^3$种,
所以满足题意的选法有$(C_2^1C_4^2+C_2^2C_4^1)A_3^3=96$(种). (4分)
(2)除去该女生后,即相当于挑选剩余的5名学生担任两科的课代表,有$A_5^2=20$(种)选法.(8分)
(3)从剩余的5名学生中选出2名有$C_5^2$种选法,排列方法有$C_2^1A_2^2$种,所以选法共有$C_5^2C_2^1A_2^2=40$(种). (12分)
点评 排列组合问题在实际问题中的应用,在计算时要求做到,兼顾所有的条件,先排约束条件多的元素,做的不重不漏,注意实际问题本身的限制条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
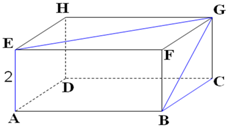 如图,已知长方体ABCD-EFGH中,AB=AD=2$\sqrt{3}$,AE=2
如图,已知长方体ABCD-EFGH中,AB=AD=2$\sqrt{3}$,AE=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
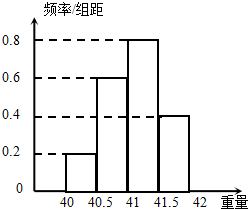 某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )
某工厂生产的200件产品的重量(单位:kg)的频率分布直方图如图所示,则重量在[40,41)的产品大约有( )| A. | 160件 | B. | 120件 | C. | 80件 | D. | 60件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com