
分析 (1)利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,可得点A,B的直角坐标,进而得到直角坐标方程,把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得极坐标方程.
(2)设M(cosθ,sinθ),则点M到直线AB距离d=$|sin(θ-\frac{π}{6})-1|$,利用三角函数的单调性值域即可得出.
解答 解:(1)由A(2,π),B(2,$\frac{π}{3}$)可得直角坐标:A(-2,0),B$(1,\sqrt{3})$.
∴直线AB的直角坐标方程为:y-0=$\frac{\sqrt{3}}{3}$(x+2),即x-$\sqrt{3}$y+2=0,
把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入可得极坐标方程:ρcosθ-$\sqrt{3}ρ$sinθ+2=0,化为:$ρsin(θ-\frac{π}{6})$=1.
(2)设M(cosθ,sinθ),
则点M到直线AB距离d=$\frac{|cosθ-\sqrt{3}sinθ+2|}{2}$=$|sin(θ-\frac{π}{6})-1|$≤2,
当且仅当$sin(θ-\frac{π}{6})$=-1时取等号,
∴点M到直线AB距离的最大值为2.
点评 本题考查了极坐标与直角坐标方程的互化、圆的方程与直线方程的应用、点到直线的距离公式、三角函数求值,考查了推理能力与计算能力,属于中档题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
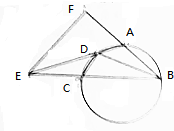 如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
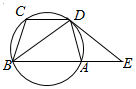 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<3x | B. | $\frac{1}{{{x^2}-x+1}}$>$\frac{1}{{{x^2}+x+1}}$ | ||
| C. | $\frac{1}{{{x^2}+1}}$>$\frac{1}{{{x^2}+2}}$ | D. | 2|x|<x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 实轴长为$4\sqrt{2}$,虚轴长为2 | B. | 实轴长为$8\sqrt{2}$,虚轴长为4 | ||
| C. | 实轴长为2,虚轴长为$4\sqrt{2}$ | D. | 实轴长为4,虚轴长为$8\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | -9 | C. | 9 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com