
分析 (1)利用平面向量的坐标运算求出$\overrightarrow{a}$-$\overrightarrow{b}$与${|\overrightarrow{a}-\overrightarrow{b}|}^{2}$,即可求出f(x)的解析式;
(2)化简函数h(x),利用换元法与分类讨论法求出函数h(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]的最值即可.
解答 解:(1)∵$\overline{a}$=(1-cosx,2sin$\frac{x}{2}$),$\overline{b}$=(1+cosx,-2cos$\frac{x}{2}$),
∴$\overrightarrow{a}$-$\overrightarrow{b}$=(-2cosx2sin$\frac{x}{2}$+2cos$\frac{x}{2}$),
${|\overrightarrow{a}-\overrightarrow{b}|}^{2}$=4cos2x+4${(sin\frac{x}{2}+cos\frac{x}{2})}^{2}$=4cos2x+4(1+sinx),
∴f(x)=2-sinx-$\frac{1}{4}$|$\overline{a}$-$\overline{b}$|2=2-sinx-$\frac{1}{4}$(4cos2x+4+4sinx)=sin2x-2sinx;
(2)函数h(x)=-sin2x-2sinx-λf(x)+1
=-sin2x-2sinx-λ(sin2x-2sinx)+1
=-(1+λ)sin2x-2(1-λ)sinx+1,
设sinx=t,则g(t)=-(1+λ)t2-2(1-λ)t+1,(-1≤t≤1);
当λ=-1时,g(t)=-4t+1在[-1,1]上是减函数;
当λ<-1时,-(1+λ)>0,g(t)为开口向上的抛物线,
其对称轴方程为直线t=$\frac{λ-1}{λ+1}$=1-$\frac{2}{λ+1}$>1,g(t)在[-1,1]上是减函数;
当-1<λ≤0时,-1<-(1+λ)<0,g(t)为开口向下的抛物线,
其对称轴方程为t=$\frac{λ-1}{λ+1}$=1-$\frac{2}{λ+1}$<-1,g(t)在[-1,1]上是减函数;
综上所述,当λ≤0时g(t)在[-1,1]上是减函数,
所以ymax=g(-1)=2-3λ,ymin=g(1)=λ-2.
点评 本题考查了三角函数的化简与求解析式的应用问题,也考查了函数的单调性与最值问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
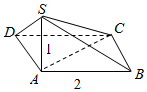 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,∠ADC=60°,SA=1,AB=2,SB=$\sqrt{5}$,平面SAB⊥底面ABCD,直线SC与底面ABCD所成的角为30°
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,∠ADC=60°,SA=1,AB=2,SB=$\sqrt{5}$,平面SAB⊥底面ABCD,直线SC与底面ABCD所成的角为30°查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com