
分析 (I)利用正切的和差公式即可得出.
(II)利用余弦定理、基本不等式的性质与三角形面积计算公式即可得出.
解答 解:(I)∵$tan\frac{A}{2}tan\frac{B}{2}+\sqrt{3}({tan\frac{A}{2}+tan\frac{B}{2}})=1$,
∴$\sqrt{3}({tan\frac{A}{2}+tan\frac{B}{2}})=1-tan\frac{A}{2}tan\frac{B}{2}$,$\frac{{tan\frac{A}{2}+tan\frac{B}{2}}}{{1--tan\frac{A}{2}tan\frac{B}{2}}}=\frac{{\sqrt{3}}}{3}$,
即 $tan({\frac{A}{2}+\frac{B}{2}})=\frac{{\sqrt{3}}}{3}$,
∵A、B为△ABC内角,
∴$\frac{A+B}{2}=\frac{π}{6}$,即 $A+B=\frac{π}{3}$.
于是 $C=π-(A+B)=\frac{2π}{3}$.
(II)证明:由用余弦定理,有${c^2}={a^2}+{b^2}-2abcosC={a^2}+{b^2}-2abcos\frac{2π}{3}={a^2}+{b^2}+ab≥3ab$,
∵△ABC的面积$S=\frac{1}{2}absinC=\frac{1}{2}absin\frac{2π}{3}=\frac{{\sqrt{3}}}{4}ab$,
∴$4\sqrt{3}S=3ab$,于是 ${c^2}≥4\sqrt{3}S$.
点评 本题考查了正切的和差公式、余弦定理、基本不等式的性质与三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
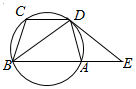 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | -9 | C. | 9 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | C. | A∪B=R | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| $\overline{x}$=1.56,$\overline{w}$=4.01,$\overline{y}$=6,$\sum_{i=1}^{5}$xiyi=48.66,$\sum_{i=1}^{5}$wiyi=132.62,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=0.20,$\sum_{i=1}^{5}$(wi-$\overline{w}$)2=10.14 | ||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com