
 如图:已知四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠C1CB=∠C1CD=∠BCD=60°,且C1C=CD=1.
如图:已知四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠C1CB=∠C1CD=∠BCD=60°,且C1C=CD=1.分析 (1)利用向量线性运算的几何意义得出,通过计算${\overrightarrow{C{A}_{1}}}_{\;}$2得出|$\overrightarrow{C{A}_{1}}$|;
(2)通过计算$\overrightarrow{C{C}_{1}}•\overrightarrow{BD}$=0得出CC1⊥BD;
(3)通过计算数量积证明CA1⊥BD,CA1⊥BC1,于是直线A1C⊥平面C1BD.
解答 解:(1)$\overrightarrow{C{A}_{1}}$=$\overrightarrow{C{C}_{1}}$+$\overrightarrow{CB}+\overrightarrow{CD}$,
${\overrightarrow{C{A}_{1}}}^{2}$=${\overrightarrow{C{C}_{1}}}^{2}$+${\overrightarrow{CB}}^{2}$+${\overrightarrow{CD}}^{2}$+2$\overrightarrow{CB}•\overrightarrow{CD}$+2$\overrightarrow{CB}•\overrightarrow{C{C}_{1}}$+2$\overrightarrow{CD}•\overrightarrow{C{C}_{1}}$
=1+1+1+2×1×1×$\frac{1}{2}$+2×1×1×$\frac{1}{2}$+2×1×1×$\frac{1}{2}$=6,
∴$|{\overrightarrow{C{A_1}}}|=\sqrt{6}$.
证明:(2)∵$\overrightarrow{C{C}_{1}}•\overrightarrow{BD}$=$\overrightarrow{C{C}_{1}}$•($\overrightarrow{CD}-\overrightarrow{CB}$)=$\overrightarrow{C{C}_{1}}$•$\overrightarrow{CD}$-$\overrightarrow{C{C}_{1}}$•$\overrightarrow{CB}$=$1×1×\frac{1}{2}-1×1×\frac{1}{2}$=0,
∴$\overrightarrow{C{C_1}}⊥\overrightarrow{BD}$,
∴CC1⊥BD.
(3)$\overrightarrow{C{A}_{1}}$$•\overrightarrow{BD}$=($\overrightarrow{C{C}_{1}}$+$\overrightarrow{CB}+\overrightarrow{CD}$)•($\overrightarrow{CD}-\overrightarrow{CB}$)
=${\overrightarrow{CD}^2}-\overrightarrow{CB}•\overrightarrow{CD}+\overrightarrow{CB}•\overrightarrow{CD}-{\overrightarrow{CB}^2}+\overrightarrow{C{C_1}}•\overrightarrow{CD}-\overrightarrow{CB}•\overrightarrow{C{C_1}}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-1+$\frac{1}{2}$$-\frac{1}{2}$=0,
∴$\overrightarrow{C{A_1}}⊥\overrightarrow{BD}$,∴CA1⊥BD.
同理可证CA1⊥BC1,
∵BC1?面BDC1,BD?面BDC1,BC1∩BD=B,
∴A1C⊥面C1DB.
点评 本题考查了空间向量在立体几何中的应用,属于中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {1,2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCD-EFQH材料切割成三棱锥H-ACF.
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCD-EFQH材料切割成三棱锥H-ACF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
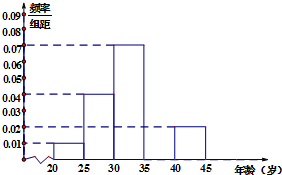 随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.
随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | 20 | 0.20 |
| [30,35) | ① | 0.350 |
| [35,40) | 30 | ② |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥CD,BC=6,cos∠ABC=-$\frac{1}{3}$.
如图,在梯形ABCD中,AB∥CD,BC=6,cos∠ABC=-$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com