
分析 运用所学知识逐个判断真假.①写出逆命题,再判断真假;②采用正弦定理推导;③特称命题的否定,改条件,否结论;④单调性法结合零点存在性定理判断.若用数形结合构造函数作函数y=x和y=sinx的图象,对y=sinx作图不规范,容易画出3个交点,从而认为是3个零点,而导致错误,此命题易错;⑤方程思想联立方程组计算可得.
解答 解:分别判断命题①至⑤真假如下;
命题①:“若x=$\frac{π}{6}$,则sinx=$\frac{1}{2}$”的逆命题为“若sinx=$\frac{1}{2}$,则$x=\frac{π}{6}$”是假命题.
解方程sinx=$\frac{1}{2}$,得:$x=\frac{π}{6}+2kπ$或$x=\frac{5π}{6}+2kπ$(k∈Z),
∴所以命题①不正确.
命题②:在△ABC中,设角A、B、C的对边分别为a、b、c,
由正弦定理:$\frac{a}{sinA}=\frac{b}{sinB}$且 sinA>sinB,
∴a>b,
又∵三角形ABC中,大边对大角,小边对小角,
∴A>B
故命题②是真命题,即命题②正确.
命题③:命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R,都有x2+x+1≥0”,
故命题③不正确.
命题④:对函数求导得f′(x)=1-cosx≥0,知f(x)为R上的增函数,
又有f(0)=0,
所以,函数f(x)在R上有且只有一个零点.
故命题④正确.
命题⑤:设扇形半径为R,扇形弧长为L,周长为C,面积为S,扇形中心角为α,
列方程组如下:
$\left\{\begin{array}{l}{C=2R+L}\\{L=αR}\\{S=\frac{1}{2}LR}\end{array}\right.$解得:$\left\{\begin{array}{l}{L=2}\\{R=2}\\{α=1}\end{array}\right.$或$\left\{\begin{array}{l}{L=4}\\{R=1}\\{α=4}\end{array}\right.$,
∴扇形中心角为1或4,命题⑤不正确.
故答案为:②④.
点评 本题涉及知识面比较广,要求对各模块知识点掌握,但各命题判断难度不大,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{3\sqrt{6}}}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(-∞,1)上是增函数,在(1,+∞)上是增函数 | |
| B. | 减函数 | |
| C. | 在(-∞,1)上是减函数,在(1,+∞)上是减函数 | |
| D. | 增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
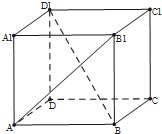
| A. | 45° | B. | 90° | C. | 60° | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com