
| A. | 45° | B. | 90° | C. | 60° | D. | 以上答案都不对 |
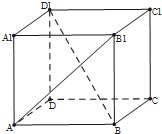
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出面对角线AB1与体对角线BD1所成角的大小.
解答 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为1,
则A(1,0,0),B1(1,1,1),B(1,1,0),D1(0,0,1),
$\overrightarrow{A{B}_{1}}$=(0,1,1),$\overrightarrow{B{D}_{1}}$=(-1,-1,1),
∵$\overrightarrow{A{B}_{1}}$•$\overrightarrow{B{D}_{1}}$=0-1+1=0,
∴面对角线AB1与体对角线BD1所成角为90°.
故选:B.
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,甲比乙成绩稳定 | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,乙比甲成绩稳定 | ||
| C. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,乙比甲成绩稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com