练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知集合M={1，-2，3}，N={-4，5，6，-7}，从两个集合中各取一个元素作为点的坐标，则在直角坐标系中，第一、第二象限不同点的个数为14．

    分析 本题首先分类在每一类中又分步，M中的元素作点的横坐标，N中的元素作点的纵坐标，N中的元素作点的横坐标，M中的元素作点的纵坐标，分别可以得到在第一和第二象限中点的个数，根据分类加法原理得到结果．

    解答 解：由题意知本题是一个分类和分步的综合问题，
    M中的元素作点的横坐标，N中的元素作点的纵坐标，在第一象限的点共有2×2个，
    在第二象限的点共有1×2个．
    N中的元素作点的横坐标，M中的元素作点的纵坐标，在第一象限的点共有2×2个，
    在第二象限的点共有2×2个．
    ∴所求不同的点的个数是2×2+1×2+2×2+2×2=14（个）．
    故答案为：14．

    点评 本题考查分步计数原理和分类计数原理，是一个综合题目，首先分类，每类方法并不都是一步完成的，必须在分类后又分步，综合利用两个原理解决．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

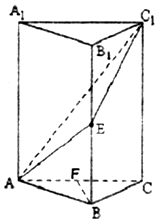    6．正三棱柱ABC-A1B1C1中，E为BB1的中点，F为AC的中点，AA1=2AB．
    （1）求证：BF∥平面AEC1；
    （2）求证：平面AEC1⊥平面A1C1CA．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

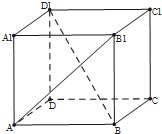
    9．如图所示，在正方体ABCD-A1B1C1D1中，直线AB1与直线BD1所成的角的大小为（　　）
    A．45°B．90°C．60°D．以上答案都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若函数f（2x）的定义域为（-2，5），则函数f（x-2）的定义域为（　　）
    A．（-3，$\frac{1}{2}$）B．（-2，12）C．（1，$\frac{9}{2}$）D．（-4，10）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知a=log${\;}_{\frac{1}{3}}$2，b=2${\;}^{-\frac{1}{3}}$，c=ln3，则（　　）
    A．a＞b＞cB．b＞a＞cC．c＞b＞aD．c＞a＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知a为锐角，且7sinα=2cos2α，则sin（α+$\frac{π}{3}$）=（　　）
    A．$\frac{{1+3\sqrt{5}}}{8}$B．$\frac{{1+5\sqrt{3}}}{8}$C．$\frac{{1-3\sqrt{5}}}{8}$D．$\frac{{1-5\sqrt{3}}}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

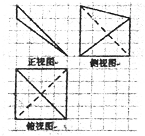    10．如图，网格上小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的棱长不可能为（　　）
    A．$4\sqrt{2}$B．$\sqrt{41}$C．$3\sqrt{2}$D．$\sqrt{17}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数y=sin4x+$\sqrt{3}$cos4x的图象的相邻两个对称中心间的距离为（　　）
    A．$\frac{π}{8}$B．$\frac{π}{4}$C．$\frac{π}{2}$D．π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知复数z=$\frac{{a}^{2}-7a+6}{{a}^{2}-1}$+（a2-5a-6）i（a∈R），试求实数a分别取什么值时，对应的点
    （1）在实轴上；
    （2）位于复平面第一象限；
    （3）在直线x+y=0上．

    查看答案和解析>>

    同步练习册答案