练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．求值：
    （1）${8^{\frac{2}{3}}}-{（{0.5}）^{-3}}+{（{\frac{1}{{\sqrt{3}}}}）^{-2}}×{（{\frac{81}{16}}）^{-\frac{1}{4}}}$；
    （2）$lg5•lg8000+{（{lg{2^{\sqrt{3}}}}）^2}+{e^{ln1}}+ln（{e\sqrt{e}}）$．

    分析 （1）利用有理数指数幂性质、运算法则求解．
    （2）利用对数性质、运算法则求解．

    解答 解：（1）${8^{\frac{2}{3}}}-{（{0.5}）^{-3}}+{（{\frac{1}{{\sqrt{3}}}}）^{-2}}×{（{\frac{81}{16}}）^{-\frac{1}{4}}}$
    =4-8+2=-2．…（6分）
    （2）$lg5•lg8000+{（{lg{2^{\sqrt{3}}}}）^2}+{e^{ln1}}+ln（{e\sqrt{e}}）$=$lg5（{3+3lg2}）+3{（{lg2}）^2}+1+\frac{3}{2}$
    =$3lg5+3lg2（{lg5+lg2}）+\frac{5}{2}$
    =3（lg5+lg2）+$\frac{5}{2}$=$\frac{11}{2}$．…（12分）

    点评 本题考查有理数指数幂、对数的化简求值，是基础题，解题时要认真审题，注意有理指数幂、对数的性质及运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．给出下列关系：①$\frac{1}{2}$∈Z；②$\sqrt{2}$∈Q；③|-3|∈N+；④3.14∈Q；⑤0∈∅，其中正确的个数为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知函数f（x）对任意实数x，y满足f（x）+f（y）=f（x+y）+3，f（3）=6，当x＞0时，f（x）＞3，那么，当f（a2-a-5）＜4时，实数a的取值范围是（-2，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

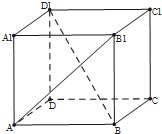
    9．如图所示，在正方体ABCD-A1B1C1D1中，直线AB1与直线BD1所成的角的大小为（　　）
    A．45°B．90°C．60°D．以上答案都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知长方体ABCD-A1B1C1D1中，AA1=AB=2，若棱AB上存在点P使D1P⊥PC，则棱AD的长的取值范围是0＜AD≤1；此时若AD取得最大值时，长方体外接球的表面积为9π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若函数f（2x）的定义域为（-2，5），则函数f（x-2）的定义域为（　　）
    A．（-3，$\frac{1}{2}$）B．（-2，12）C．（1，$\frac{9}{2}$）D．（-4，10）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知a=log${\;}_{\frac{1}{3}}$2，b=2${\;}^{-\frac{1}{3}}$，c=ln3，则（　　）
    A．a＞b＞cB．b＞a＞cC．c＞b＞aD．c＞a＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

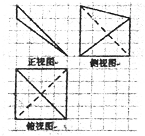    10．如图，网格上小正方形的边长为1，粗线画出的是某空间几何体的三视图，则该几何体的棱长不可能为（　　）
    A．$4\sqrt{2}$B．$\sqrt{41}$C．$3\sqrt{2}$D．$\sqrt{17}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

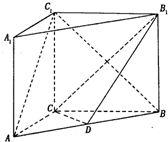    11．如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，
    （1）求证：AC⊥BC1；
    （2）求证：AC1∥平面CDB1．

    查看答案和解析>>

    同步练习册答案