
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先要弄清题中大写字母表示的数集的含义:R表示实数集,Q表示有理数集,N*表示正整数集,Z表示整数集,在这些概念的基础之上,再对四个命题加以判断,就不难得出正确命题的个数了.
解答 解:①$\frac{1}{2}$是分数,不是自然数,故$\frac{1}{2}$∈Z错误;
②$\sqrt{2}$是无理数,不是有理数,故$\sqrt{2}$∈Q错误;
③|-3=3,3是正整数,故|3||∈N+正确;
④3.14是有理数,故3.14∈Q正确;
⑤0∉∅,故0∈∅错误,
综上所述,正确的个数是2个.
故选:B.
点评 本题借助于几个数所属数集的关系,着重考查了集合的元素与集合的关系和大写字母表示数集的含义等知识点,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
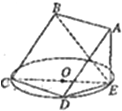 如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE为9.
如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径CE为9.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com