
分析 (Ⅰ)对f(x)进行求导,将其转化为在区间[$\frac{1}{4}$,2]上存在于区间使得不等式g(x)>0恒成立,根据抛物线的性质可以看出,图象开口向上,利用根与系数的关系进行求解;
(Ⅱ)求出函数的导数,通过讨论k的范围结合函数的单调性确定k的范围即可.
解答 解:(Ⅰ)f′(x)=$\frac{1}{x}$+2x-a=$\frac{{2x}^{2}-ax+1}{x}$,设g(x)=2x2-2ax+1
由题意知,在区间[$\frac{1}{4}$,2]上存在区间使得不等式g(x)>0恒成立,
由于抛物线g(x)=2x2-ax+1开口向上,
∴只要g(2)>0,或g($\frac{1}{4}$)>0即可,
由g(2)>0,即8-2a+1>0,∴a<$\frac{9}{2}$,
由g($\frac{1}{4}$)>0,即$\frac{1}{8}$-$\frac{1}{4}$a+1>0,∴a<$\frac{9}{2}$,
∴$a<\frac{9}{2}$;
(Ⅱ)g(x)=f(x)+2ln$\frac{ax+2}{{6\sqrt{x}}}$=2ln(ax+2)+x2-ax-2ln6,
∴g′(x)=$\frac{2ax(x+\frac{4{-a}^{2}}{2a})}{ax+2}$,
∵$\frac{4{-a}^{2}}{2a}$=$\frac{2}{a}$-$\frac{a}{2}$>-$\frac{3}{2}$,而x≥$\frac{3}{2}$,∴x+$\frac{4{-a}^{2}}{2a}$>0,
∴g′(x)>0,g(x)在x∈[$\frac{3}{2}$,2]递增,
∴g(x)max=g(2)=2ln(2a+2)-2a+4-2ln6,
∴2ln(2a+2)-2a+4-2ln6>k(4-a2)在(2,4)上恒成立.
令h(a)=2ln(2a+2)-2a+4-2ln6-k(4-a2),因h(2)=0,
∴h(a)>0在(2,4)上恒成立.
∵h′(a)=$\frac{2a(ka+k-1)}{a+1}$,
k≤0时,h′(a)<0,h(a)在(2,4)上单调递减,
h(a)<h(2)=0,不合题意;
k>0时,h′(a)=0,可得a=$\frac{1-k}{k}$.
①$\frac{1-k}{k}$>2,即0<k<$\frac{1}{3}$时,h(a)在(2,$\frac{1-k}{k}$)上单调递减,
存在h(a)<h(2)=0,不合题意;
②$\frac{1-k}{k}$≤2,即k≥$\frac{1}{3}$时,h(x)在(2,4)上单调递增,
h(a)>h(2)=0,满足题意.
综上,实数k的取值范围为[$\frac{1}{3}$,+∞).
点评 此题主要考查利用导数研究求闭区间上的最值问题,此题综合性比较强,这类题型是高考的热点问题,解的过程中我们用到了分类讨论和转化的思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(n+1)(n+2)}{2}$ | B. | $\frac{n(n+1)}{2}$ | C. | $\frac{n}{n+1}$ | D. | $\frac{n}{n+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\sqrt{6}$ | C. | $\frac{{3\sqrt{6}}}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
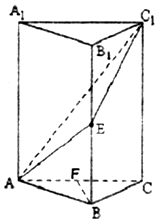 正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
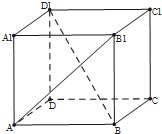
| A. | 45° | B. | 90° | C. | 60° | D. | 以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com