
 ����������ѧ��ȤС���ͬѧ��������ǰģ�⿼�ԣ��ɼ���¼���£���λ���֣���
����������ѧ��ȤС���ͬѧ��������ǰģ�⿼�ԣ��ɼ���¼���£���λ���֣������� ��1�������ݷ��������
��2������ƽ���ֺͷ�����ݷ����С�Ƚ��ȶ��ԣ�
��� �⣺��1���ɼ�������ijɼ���¼�������ס�����λѧ���ɼ��ľ�Ҷͼ���£�
��2������ͬѧ�ɼ���ƽ����$\overline{{x}_{��}}$=$\frac{1}{8}$��79+81+82+78+95+93+84+88��=85��
����ͬѧ�ɼ��ķ���S��2=$\frac{1}{8}$[��79-85��2+��81-85��2+��82-85��2+��78-85��2+��95-85��2+��93-85��2+��84-85��2+��88-85��2]=35.5��
����ͬѧ�ɼ���ƽ����$\overline{{x}_{��}}$=$\frac{1}{8}$��95+80+92+83+75+85+90+80��=85��
����ͬѧ�ɼ��ķ���S��2=$\frac{1}{8}$[��95-85��2+]��80-85��2+��92-85��2+��83-85��2+��75-85��2+��85-85��2+��90-85��2+��80-85��2]=41��
��������ͬѧ�ɼ���ƽ������ȣ�����ͬѧ�ɼ��ķ�����ڼ���ͬѧ�ɼ��ķ��
�����ͬѧģ�⿼���з��ӱȽ��ȶ���
���� ���⿼���˾�Ҷͼ��������㣬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
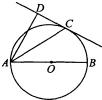 ��ͼ����֪AB�ǡ�O��ֱ����ֱ��CD���O�����ڵ�C��AD��CD��
��ͼ����֪AB�ǡ�O��ֱ����ֱ��CD���O�����ڵ�C��AD��CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
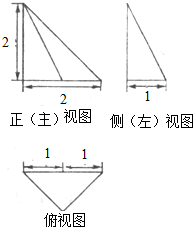
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �����Ա� | �� | Ů | �ܼ� |
| ѡ���� | 40 | 20 | 60 |
| ѡ�Ŀ� | 10 | 30 | 40 |
| �ܼ� | 50 | 50 | 100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [$\frac{��}{6}$+2k��$\frac{5��}{6}$+2k��]��k��Z | B�� | [-$\frac{��}{6}$+2k��$\frac{7��}{6}$+2k��]��k��Z | ||
| C�� | [$\frac{��}{3}$+2k��$\frac{2��}{3}$+2k��]��k��Z | D�� | [-$\frac{��}{3}$+2k��$\frac{4��}{3}$+2k��]��k��Z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com