
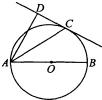
 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD.分析 (1)利用圆的性质、圆的切线的性质,可得∠ADC=∠ACB=90°.∠DCA=∠B.可得△ADC∽△ACB,即可证明.
(2)由(1)得△ADC∽△ACB.利用相似的性质即可得出.
解答 (1)证明:连接BC.由AB为⊙O的直径,得∠ACB=90°.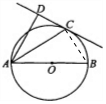
∵AD⊥CD,∴∠ADC=∠ACB=90°.
∵直线CD与⊙O相切于点C,
∴∠DCA=∠B.
∴△ADC∽△ACB,∴∠CAD=∠BAC.
(2)解:由(1)得△ADC∽△ACB.
∴$\frac{AD}{AC}=\frac{AC}{AB}$,∴AC2=AD•AB.
又∵AD=4,AC=6,∴AB=9.
点评 本题考查了圆的性质、圆的切线的性质、相似三角形的判定与性质定理,考查了推理能力与计算能力,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
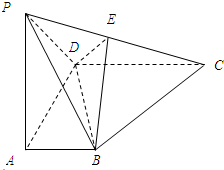 如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点
如图,四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥面ABCD,E为PC中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示:O、A、B是平面上的三点,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2在平面AOB上,若P为线段AB的中垂线上任意一点,则$\overrightarrow{OP}$•($\overrightarrow{a}$-$\overrightarrow{b}$)的值是( )
如图所示:O、A、B是平面上的三点,设向量$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=2在平面AOB上,若P为线段AB的中垂线上任意一点,则$\overrightarrow{OP}$•($\overrightarrow{a}$-$\overrightarrow{b}$)的值是( )| A. | $\frac{5}{2}$ | B. | 5 | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M={2,3},S={(2,3)} | |
| B. | M={π},S={3.14} | |
| C. | M={0},S=∅ | |
| D. | M={1,2,3,…,n-1,n},S={前n个非零自然数} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}-1}}{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com