
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
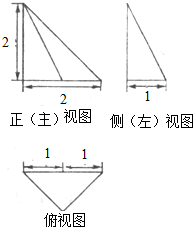
分析 根据几何体的三视图,得出该几何体是直三棱锥,根据图中的数据,求出该三棱锥的4个面的面积,得出面积最大的三角形的面积.
解答 解:根据几何体的三视图,得该几何体是如图所示的直三棱锥, 且侧棱PA⊥底面ABC,
且侧棱PA⊥底面ABC,
PA=2,AC=2,点B到AC的距离为1;
∴底面△ABC的面积为S1=$\frac{1}{2}$×2×1=1,
侧面△PAB的面积为S2=$\frac{1}{2}×\sqrt{2}×2$=$\sqrt{2}$,
侧面△PAC的面积为S3=$\frac{1}{2}$×2×2=2,
在侧面△PBC中,BC=$\sqrt{2}$,PB=$\sqrt{6}$,PC=2$\sqrt{2}$,
∴△PBC是Rt△,
∴△PBC的面积为S4=$\frac{1}{2}$×$\sqrt{2}×\sqrt{6}$=$\sqrt{3}$;
∴三棱锥P-ABC的所有面中,面积最大的是△PAC,为2
故选:D.
点评 本题考查了空间几何体的三视图的应用问题,也考查了空间中的位置关系与距离的计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | M={2,3},S={(2,3)} | |
| B. | M={π},S={3.14} | |
| C. | M={0},S=∅ | |
| D. | M={1,2,3,…,n-1,n},S={前n个非零自然数} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $-\frac{{\sqrt{2}}}{2}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
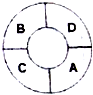 如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )
如图,一环形花坛成A,B,C,D四块,现有4种不同的花供选择,要求在每块地里种一种花,且相邻的两块种不同的花,则不同的种法总数为( )| A. | 48 | B. | 60 | C. | 84 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{(n+1)(n+2)}{2}$ | B. | $\frac{n(n+1)}{2}$ | C. | $\frac{n}{n+1}$ | D. | $\frac{n}{n+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
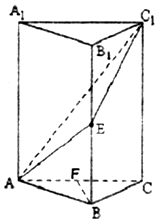 正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.
正三棱柱ABC-A1B1C1中,E为BB1的中点,F为AC的中点,AA1=2AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com