
分析 (1)根据复合函数的单调性求解即可.
(2)根据计算的函数值,找个其周期规律,从而求解.
(3)利用换元法,转化成二次函数问题求解.
解答 解:(1)由题意:函数f(x)=log2(sin($\frac{π}{3}$x+$\frac{π}{3}$)),
令u=sin($\frac{π}{3}$x+$\frac{π}{3}$),则f(x)=log2u是增函数.
∵u>0,即$sin(\frac{π}{3}x+\frac{π}{3})>0$,
可得:$\frac{π}{3}x+\frac{π}{3}∈(2kπ,π+2kπ),k∈Z$
解得:x∈(-1+6k,2+6k),k∈Z
∴函数f(x)的定义域为x∈(-1+6k,2+6k),k∈Z
当$\frac{π}{3}x+\frac{π}{3}∈(\frac{π}{2}+2kπ,π+2kπ),k∈Z$时,函数u=sin($\frac{π}{3}$x+$\frac{π}{3}$)是减函数,
解得:$x∈(\frac{1}{2}+6k,2+6k),k∈Z$
∴函数f(x)的单调递减区间为$x∈(\frac{1}{2}+6k,2+6k),k∈Z$.
(2)由题意:令$h(x)=sin(\frac{π}{3}x+\frac{π}{3})$,是周期函数T=6,计算可得h(1)+h(3)+h(5)=0,
∴h(7)+h(9)+h(11)=0…
∴h(1)+h(3)+h(5)=h(7)+h(9)+h(11)=…=h(2011)+h(2013)+h(2015)=0
∴h(1)+h(3)+h(5)+…+h(2015)=0
(3)g(x)=4f(x)+2f(x)+1,
令t=2f(x),由题意可知t∈(0,1]
那么:g(x)=4f(x)+2f(x)+1,
转化为g(t)=t2+t+1(t∈(0,1]),
g(t)在(0,1]上单调递增,
g(t)∈(1,3],
所以:g(x)的值域为(1,3].
点评 本题考查了复合函数的单调性“同增异减”和周期性函数的求值问题以及复合函数值域的问题.属于中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
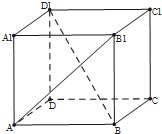
| A. | 45° | B. | 90° | C. | 60° | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=2,φ=$\frac{π}{4}$ | B. | ω=2,φ=$\frac{π}{2}$ | C. | ω=1,φ=$\frac{π}{2}$ | D. | ω=1,φ=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,$\frac{1}{2}$) | B. | (-2,12) | C. | (1,$\frac{9}{2}$) | D. | (-4,10) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{1+3\sqrt{5}}}{8}$ | B. | $\frac{{1+5\sqrt{3}}}{8}$ | C. | $\frac{{1-3\sqrt{5}}}{8}$ | D. | $\frac{{1-5\sqrt{3}}}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com