练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于区间和函数,若同时满足：①在上是单调函数；②函数， 的值域还是，则称区间为函数的“不变”区间.

    （1）求函数的所有“不变”区间.

    （2）函数是否存在“不变”区间？若存在，求出实数的取值范围；若不存在，说明理由.

    【答案】（1）（2）

    【解析】试题分析：（1）先确定函数单调性，再根据“不变”区间定义得，解得，即得“不变”区间（2）同上先确定函数单调性，再根据“不变”区间定义得，化简得，因此，最后根据函数，求实数的取值范围

    试题解析：(1)易知函数单调递增,

    故有解得 又，所以

    所以函数的“不变”区间为.

    (2)易知函数单调递增，若函数存在“不变”区间，则有，且消去得，整理得.

    因为,所以，即.

    又由得，所以.

    所以 所以.

    综上，当时,函数存在“不变”区间

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】潮州统计局就某地居民的月收入调查了人，并根据所得数据画了样本的频率分

    布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在）。

    （1）求居民月收入在的频率；

    （2）根据频率分布直方图算出样本数据的中位数；

    （3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这人中分层抽样方法抽出人作进一步分析，则月收入在的这段应抽多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）讨论函数的单调性；

    （2）当时，恒成立，求实数的取值范围；

    （3）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求证： ；

    （2）当且时，求函数的最小值；

    （3）若，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=4x2﹣4ax+a2﹣2a+2在区间[0，2]上有最小值3，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列是关于函数y＝f(x)，x∈[a，b]的几个命题：

    ①若x0∈[a，b]且满足f(x0)＝0，则(x0,0)是f(x)的一个零点；

    ②若x0是f(x)在[a，b]上的零点，则可用二分法求x0的近似值；

    ③函数f(x)的零点是方程f(x)＝0的根，但f(x)＝0的根不一定是函数f(x)的零点；

    ④用二分法求方程的根时，得到的都是近似值.

    那么以上叙述中，正确的个数为 (　　)

    A. 0 B. 1 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】否定“自然数、、中恰有一个偶数”时正确的反设为（ ）

    A. 、、都是奇数 B. 、、至少有两个偶数

    C. 、、都是偶数 D. 、、中都是奇数或至少有两个偶数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次购物抽奖活动中，假设某10张券中有一等奖1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有将；某顾客从此10张券中任取2张，求：

    （1）该顾客中奖的概率；

    （2）该顾客获得的奖品总价值（元）的概率分布列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    等腰梯形ABEF中，AB∥EF，AB＝2，AD＝AF＝1，AF⊥BF，O为AB的中点，矩形ABCD 所在的平面和平面ABEF互相垂直．

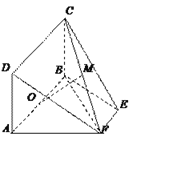
    (1)求证：AF⊥平面CBF；

    (2)设FC的中点为M，求证：OM∥平面DAF；

    (3)求三棱锥C－BEF的体积．

    查看答案和解析>>

    同步练习册答案