
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:![]() .
.
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 在
在![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 在
在 单调递增,在
单调递增,在 单调递减;(2)
单调递减;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)借助题设条件运用分类整合思想分类讨论;(2)借助题设构设函数,运用导数知识求解;(3)依据题设构设函数,建立不等式运用导数的知识分析推证.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ……2分
……2分
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减;………………4分
单调递减;………………4分
当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
则当 时,
时,![]() ;
; 时,
时,![]() .
.
故![]() 在
在 单调递增,在
单调递增,在 单调递减.……6分
单调递减.……6分
(2)因为![]() ,所以:
,所以:
当![]() 时,
时,![]() 恒成立
恒成立![]() ,
,
令![]() ,则
,则![]() ,……………………8分
,……………………8分
因为![]() ,由
,由![]() 得
得![]()
![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,所以
上递减,所以![]() ,
,
故![]() .…………………………10分
.…………………………10分
(3)取![]() ,则代入
,则代入![]() 由题设可得
由题设可得![]() ,取
,取![]() ,并将上述各不等式两边加起来可得
,并将上述各不等式两边加起来可得![]() .
.


科目:高中数学 来源: 题型:
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在多面体![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
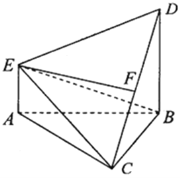
(1)若![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5名男生4名女生站成一排,求满足下列条件的排法:
(1)女生都不相邻有多少种排法?
(2)男生甲、乙、丙排序一定(只考虑位置的前后顺序),有多少种排法?
(3)男甲不在首位,男乙不在末位,有多少种排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
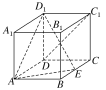
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若二面角B1AED1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于区间![]() 和函数
和函数![]() ,若同时满足:①
,若同时满足:①![]() 在
在![]() 上是单调函数;②函数
上是单调函数;②函数![]() ,
, ![]() 的值域还是
的值域还是![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的“不变”区间.
的“不变”区间.
(1)求函数![]() 的所有“不变”区间.
的所有“不变”区间.
(2)函数![]() 是否存在“不变”区间?若存在,求出实数
是否存在“不变”区间?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心在原点,其一个焦点与抛物线y2=4![]() x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.
x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.
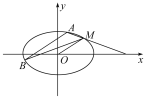
(1)求椭圆C的方程;
(2)当MA,MB与x轴所构成的三角形是以x轴上所在线段为底边的等腰三角形时,求直线l在y轴上截距的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com