
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题意,该工程施工期间降水![]() 小于
小于![]() 的概率分别为
的概率分别为![]() ,结合工程施工期间的降水量对工期的影响,可求相应的概率,金额可得延误天数
,结合工程施工期间的降水量对工期的影响,可求相应的概率,金额可得延误天数![]() 的均值与方差;(2)利用概率的加法公式,可得各个概率值,再利用条件概率,即可得到结论.
的均值与方差;(2)利用概率的加法公式,可得各个概率值,再利用条件概率,即可得到结论.
试题解析:(1)由已知条件和概率的加法公式,有
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
| 0 | 2 | 6 | 10 |
| 0.3 | 0.4 | 0.2 | 0.1 |
于是,![]() ;
;
D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8.
故工期延误天数Y的均值为3,方差为9.8,
(2)由概率的加法公式,![]() ,
,
又![]() .
.
由条件概率,得
![]() .
.
故在降水量![]() 至少是300
至少是300![]() 的条件下,工期延期不超过6天的概率是
的条件下,工期延期不超过6天的概率是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
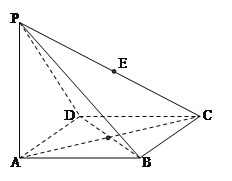
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
求数学成绩![]() 关于物理成绩
关于物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]()
若某位学生的物理成绩为80分,预测他的数学成绩;
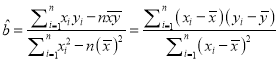
查看答案和解析>>
科目:高中数学 来源: 题型:
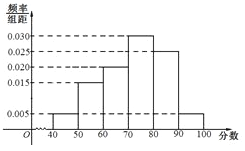
【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在![]() 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元![]() 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
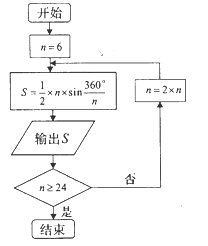
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中![]() 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
(参考数据: ![]() )
)
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com