
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
【答案】(1)2520;(2)3600;(3)1440;(4)720.
【解析】试题分析:
(1)属于从7个不同元素中任选5个的排列;
(2)第一步先安排特殊元素甲,第二步其他6人全排列即可;
(3)第一步排所有女生,第二步在5个空位(含两端)排3个男生;
(4)第一步选3人排在甲乙中间(注意这3人全排列),第二步甲乙两也全排列,第三步甲乙和他们中间的3人作为一个整体与剩下的2人变成3个元素再全排列.
试题解析:
(1)![]() =2520(种).
=2520(种).
(2)先排甲,有5种方法,其余6人有![]() 种方法,故共有5×
种方法,故共有5×![]() =3600(种).
=3600(种).
(3)男生不相邻,而女生不作要求,∴应先排女生,有![]() 种方法,
种方法,
再在女生之间及首尾空出的5个空位中任选3个空位排男生,有![]() 种方法,故共有
种方法,故共有![]() ·
·![]() =1440(种).
=1440(种).
(4)把甲、乙及中间3人看作一个整体,
第一步先排甲、乙两人有![]() 种方法,
种方法,
再从剩下的5人中选3人排到中间,有![]() 种方法,
种方法,
最后把甲、乙及中间3人看作一个整体,与剩余2人排列,有![]() 种方法,
种方法,
故共有![]() ·
·![]() ·
·![]() =720(种).
=720(种).


科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
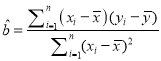 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .若点
.若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,
, ![]() ,以
,以![]() 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )在
)在![]() 上的最小值为
上的最小值为![]() ,当把
,当把![]() 的图象上所有的点向右平移
的图象上所有的点向右平移![]() 个单位后,得到函数
个单位后,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)在△![]() 中,角
中,角![]() ,
,![]() ,
,![]() 对应的边分别是
对应的边分别是![]() ,
,![]() ,
,![]() ,若函数
,若函数![]() 在
在![]() 轴右侧的第一个零点恰为
轴右侧的第一个零点恰为![]() ,
,![]() ,求△
,求△![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字
(1)求取出的3张卡片上的数字互不相同的概率;
(2)求随机变量x的分布列;
(3)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在多面体![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
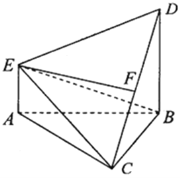
(1)若![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com