
【题目】如下图,在多面体![]() 中,
中,![]() ⊥平面
⊥平面![]() ,
,![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
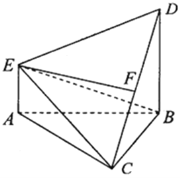
(1)若![]() 是线段
是线段![]() 的中点,证明:
的中点,证明:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】有3名男生,4名女生,在下列不同要求下,求不同的排列方法种数:
(1)选其中5人排成一排
(2)全体排成一排,甲不站在排头也不站在排尾
(3)全体排成一排,男生互不相邻
(4)全体排成一排,甲、乙两人中间恰好有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元![]() 年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值
年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中
,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中![]() 表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为 ( )
(参考数据: ![]() )
)
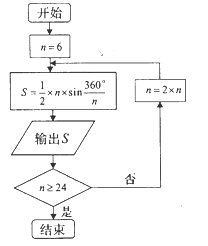
A. 2.598,3,3.1048 B. 2.598,3,3.1056
C. 2.578,3,3.1069 D. 2.588,3,3.1108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() =2.71828……是自然对数的底数),曲线
=2.71828……是自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的值;
的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() ,其中
,其中![]() 是
是![]() 的导函数.证明:对任意
的导函数.证明:对任意![]() >0,
>0,![]() <
<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】否定“自然数![]() 、
、![]() 、
、![]() 中恰有一个偶数”时正确的反设为( )
中恰有一个偶数”时正确的反设为( )
A. ![]() 、
、![]() 、
、![]() 都是奇数 B.
都是奇数 B. ![]() 、
、![]() 、
、![]() 至少有两个偶数
至少有两个偶数
C. ![]() 、
、![]() 、
、![]() 都是偶数 D.
都是偶数 D. ![]() 、
、![]() 、
、![]() 中都是奇数或至少有两个偶数
中都是奇数或至少有两个偶数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com