
| A. | m∥l,m⊥α | B. | m∥l,m∥α | C. | m⊥l,m⊥α | D. | m⊥l,m∥α |
 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:选择题
| A. | {-1,0} | B. | {0,3} | C. | {-1,3} | D. | {-1,0,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
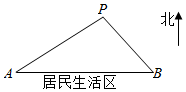 如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):
如图所示,A,B是两个垃圾中转站,B在A的正东方向16千米处,AB的南面为居民生活区,为了妥善处理生活垃圾,政府决定在AB的背面建一个垃圾发电厂P,垃圾发电厂P的选址拟满足以下两个要求(A,B,P可看成三个点):查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
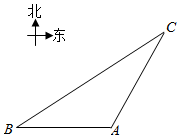 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com