
分析 ①由blna-alnb=a-b得$\frac{1+lna}{a}$=$\frac{1+lnb}{b}$,构造函数f(x)=$\frac{1+lnx}{x}$,x>0,判断a,b的取值范围即可.
②由对数平均不等式进行证明,
③构造函数,判断函数的单调性,进行证明即可.
解答 解:①由blna-alnb=a-b,得blna+b=alnb+a,即$\frac{1+lna}{a}$=$\frac{1+lnb}{b}$,
设f(x)=$\frac{1+lnx}{x}$,x>0,
则f′(x)=$\frac{\frac{1}{x}•x-(1+lnx)}{{x}^{2}}$=$\frac{-lnx}{{x}^{2}}$,
由f′(x)>0得-lnx>0,得lnx<0,得0<x<1,
由f′(x)<0得-lnx<0,得lnx>0,得x>1,
即当x=1时,函数f(x)取得极大值,
则$\frac{1+lna}{a}$=$\frac{1+lnb}{b}$,等价为f(a)=f(b),
则a,b一个大于1,一个小于1,
不妨设0<a<1,b>1.
则a+b-ab>1等价为(a-1)(1-b)>0,
∵0<a<1,b>1.∴(a-1)(1-b)>0,则a+b-ab>1成立,故①正确,
②由$\frac{1+lna}{a}$=$\frac{1+lnb}{b}$,
得$\frac{lna+lnb+2}{a+b}$=$\frac{lna-lnb}{a-b}$,
由对数平均不等式得$\frac{lna+lnb+2}{a+b}$=$\frac{lna-lnb}{a-b}$>$\frac{2}{a+b}$,
即lna+lnb>0,即lnab>0,
则ab>1,
由均值不等式得a+b$>2\sqrt{ab}>$2,故②正确,
③令g(x)=-xlnx+x,则g′(x)=-lnx,
则由g′(x)>0得-lnx>0,得lnx<0,得0<x<1,此时g(x)为增函数,
由g′(x)<0得-lnx<0,得lnx>0,得x>1,此时g(x)为减函数,
再令h(x)=g(x)-g(2-x),0<x<1,
则h′(x)=g′(x)+g′(2-x)=-lnx-lm(2-x)=-ln[x(2-x)]>0,
则h(x)=g(x)-g(2-x),在0<x<1上为增函数,
则h(x)=g(x)-g(2-x)<h(1)=0,
则g(x)<g(2-x),
即g($\frac{1}{a}$)<g(2-$\frac{1}{a}$),
∵g($\frac{1}{a}$)=$\frac{1}{a}$-$\frac{1}{a}$ln$\frac{1}{a}$=$\frac{1}{a}$+$\frac{1}{a}$lna=$\frac{1+lna}{a}$=$\frac{1+lnb}{b}$,
∴g($\frac{1}{a}$)=g($\frac{1}{b}$)
则g($\frac{1}{b}$)=g($\frac{1}{a}$)<g(2-$\frac{1}{a}$),
∵g(x)在0<x<1上为增函数,
∴$\frac{1}{b}$>2-$\frac{1}{a}$,
即$\frac{1}{a}$+$\frac{1}{b}$>2.
故③正确,
故答案为:①②③
点评 本题主要考查命题的真假判断,涉及不等式的证明,利用构造法,结合函数的单调性和导数的关系是解决本题的关键.综合性较强,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:1 | C. | 2:1 | D. | $\sqrt{6}$:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②④ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 3 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥l,m⊥α | B. | m∥l,m∥α | C. | m⊥l,m⊥α | D. | m⊥l,m∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
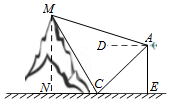 如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.
如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com