
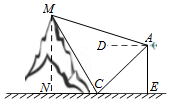
 如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.
如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m. 分析 在等腰直角△ABC中得出AC=200$\sqrt{2}$,在△AMC中使用正弦定理求出MC,解Rt△MNC得出MN.
解答 解:在Rt△ABC中,∠ACB=∠DAC=45°,∠ABC=90°,AB=200,
∴AC=200$\sqrt{2}$,
∵∠MCN=60°,∴∠ACM=180°-∠MCN-∠ACB=75°,
∵∠MAC=15°+45°=60°,∴∠AMC=180°-∠MAC-∠ACM=45°.
在△MAC中,由正弦定理得$\frac{MC}{sin∠MAC}=\frac{AC}{sin∠AMC}$,即$\frac{MC}{\frac{\sqrt{3}}{2}}=\frac{200\sqrt{2}}{\frac{\sqrt{2}}{2}}$
解得MC=200$\sqrt{3}$.
∵sin∠MCN=$\frac{MN}{MC}=\frac{\sqrt{3}}{2}$,
∴MN=$\frac{\sqrt{3}}{2}$MC=300.
故答案为:300.
点评 本题考查了正弦定理,解三角形的实际应用,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $({\frac{3π}{8},0})$ | B. | $({\frac{π}{8},0})$ | C. | $({\frac{3π}{4},0})$ | D. | $({\frac{π}{4},0})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x),g(x)都是单调函数,则h(x)也是单调函数 | |
| B. | 若f(x),g(x)都是奇函数,则h(x)也是奇函数 | |
| C. | 若f(x),g(x)都是偶函数,则h(x)也是偶函数 | |
| D. | 若f(x)是奇函数,g(x)是偶函数,则h(x)既不是奇函数,也不是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
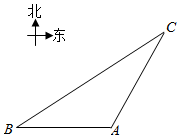 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{7}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{11}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com