练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知集合A={0，1，2，3，4}，B={x|x2-2x＞0}，则A∩B=（　　）
    A．（2，4]B．[2，4]C．{0，3，4}D．{3，4}

    分析 求出B中不等式的解集确定出B，找出A与B的交集即可．

    解答 解：由B中不等式变形得：x（x-2）＞0，
    解得：x＜0或x＞2，即B=（-∞，0）∪（2，+∞），
    ∵A={0，1，2，3，4}，
    ∴A∩B={3，4}，
    故选：D．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

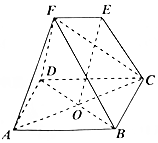    12．如图，在几何体中，四边形ABCD为菱形，对角线AC与BD的交点为O，四边形DCEF为梯形，EF∥DC，FD=FB．
    （Ⅰ）若DC=2EF，求证：OE∥平面ADF；
    （Ⅱ）求证：平面AFC⊥平面ABCD；
    （Ⅲ）若AB=FB=2，AF=3，∠BCD=60°，求AF与平面ABCD所成角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知正项数列{an}的前n项和为Sn，且$\sqrt{{S}_{n}}$是1与an的等差中项．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设Tn为数列{$\frac{2}{{a}_{n}{a}_{n+1}}$}的前n项和，证明：$\frac{2}{3}$＜Tn＜1（n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设复数z满足z（1+i）=i（i为虚数单位），则|z|=（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．1D．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC+ccosB=3acosB，b=2，且△ABC的面积为$\frac{3\sqrt{2}}{2}$，则a+c=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设直线l过双曲线C的一个焦点，且与C的一条对称轴垂直，l与C交于A，B两点，|AB|为C的实轴长的2倍，则C的离心率为$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

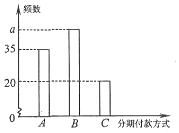    14．某知名品牌汽车深受消费者喜爱，但价格昂贵．某汽车经销商推出A，B，C三种分期付款方式销售该品牌汽车，并对近期100位采用上述分期付款的客户进行统计分析，得到如下的柱状图．已知从A，B，C三种分期付款销售中，该经销商每销售此品牌汽车1辆所获得的利润分别是1万元，2万元，3万元．以这100 位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率．
    （Ⅰ）求采用上述分期付款方式销售此品牌汽车1辆，该汽车经销商从中所获得的利润不大于2万元的概率；
    （Ⅱ）求采用上述分期付款方式销售此品牌汽车1辆，该汽车经销商从中所获得的利润的平均值；
    （Ⅲ）根据某税收规定，该汽车经销商每月（按30天计）上交税收的标准如表：
    月利润（单位：万元）在（0，100]内的部分超过100且不超过150的部分超过150的部分
    税率1%2%4%
    若该经销商按上述分期付款方式每天平均销售此品牌汽车3辆，估计其月纯收入（纯收入=总利润-上交税款）的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若$|{\overrightarrow{e_1}}|=|{\overrightarrow{e_2}}|=1$，$cos＜\overrightarrow{e_1}，\overrightarrow{e_2}＞=-\frac{1}{5}$，且$\overrightarrow a=2\overrightarrow{e_1}-\overrightarrow{e_2}，\overrightarrow b=\overrightarrow{e_1}+3\overrightarrow{e_2}$，则$\overrightarrow a•\overrightarrow b$=（　　）
    A．2B．-2C．$-\frac{1}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知n∈N*，数列{dn}满足${d_n}=\frac{{3+{{（{-1}）}^n}}}{2}$，数列{an}满足an=d1+d2+d3+…+d2n；又在数列{bn}中b1=2，且对?m，n∈N*，$b_n^m=b_m^n$．
    （ I）求数列{an}和{bn}的通项公式；
    （ II）将数列{bn}中的第a1项、第a2项、第a3项、…、第an项删去后，剩余的项按从小到大的顺序排列成新的数列{cn}，求数列{cn}的前2016项的和T2016．

    查看答案和解析>>

    同步练习册答案