
【题目】已知函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() 时,若方程
时,若方程![]() 有实根,求
有实根,求![]() 的最小值;
的最小值;
(2)设![]() ,若
,若![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
【答案】(1) 最小值为0. (2) ![]()
【解析】
(1)当![]() 时,利用导数求得
时,利用导数求得![]() 的最小值为
的最小值为![]() ,所以
,所以![]() ,故
,故![]() 的最小值为
的最小值为![]() .
.
(2)首先求得![]() 的解析式,利用二次求导的方法,结合
的解析式,利用二次求导的方法,结合![]() 在区间
在区间![]() 上是单调函数,将
上是单调函数,将![]() 分成
分成![]() 和
和![]() 两种情况进行分类讨论,由此求得
两种情况进行分类讨论,由此求得![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
∴![]() .
.
由![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() .即
.即![]() 的最小值为0.
的最小值为0.
(2)∵![]() ,∴
,∴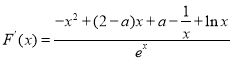 .
.
设![]() ,则
,则![]() ,
,
可知![]() 在
在![]() 上为减函数.
上为减函数.
从而![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上为增函数,
上为增函数,
∵![]() ,∴
,∴![]() 在区间
在区间![]() 上恒成立,即
上恒成立,即![]() 在区间
在区间![]() 上恒成立.
上恒成立.
∴![]() 在区间
在区间![]() 上是减函数,故
上是减函数,故![]() 满足题意;
满足题意;
②当![]() ,即
,即![]() 时,设函数
时,设函数![]() 的唯一零点为
的唯一零点为![]() ,
,
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴
,∴![]() 在
在![]() 上递减,
上递减,
这与![]() 在区间
在区间![]() 上是单调函数矛盾.
上是单调函数矛盾.
∴![]() 不合题意.
不合题意.
综合①②得:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 底面是直角梯形,点E是棱PC的中点,
底面是直角梯形,点E是棱PC的中点,![]() ,
,![]() 底面ABCD,
底面ABCD,![]() .
.
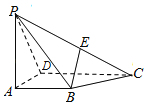
(1)判断BE与平面PAD是否平行,证明你的结论;
(2)证明:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积V.
的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() , 过点
, 过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于M、N两点(M点在N点的上方),与
交于M、N两点(M点在N点的上方),与![]() 轴交于点E.
轴交于点E.
(1)当![]() 且
且![]() 时,求点M、N的坐标;
时,求点M、N的坐标;
(2)当![]() 时,设
时,设![]() ,
,![]() ,求证:
,求证:![]() 为定值,并求出该值;
为定值,并求出该值;
(3)当![]() 时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于
时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为![]() ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(1)求f(x)的表达式
(2)宿舍应建在离工厂多远处,可使总费用f(x)最小并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 上的点
上的点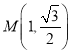 对应的参数
对应的参数![]() .在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.射线
是圆心在极轴上,且经过极点的圆.射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() ,
,![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}满足:a3+a8=20,且a5是a2与a14的等比中项.
(1)求数列{an}的通项公式;
(2)设数列{bn}满足![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,四边形ABCD菱形,![]() ,平面
,平面![]() 平面 ABCD,
平面 ABCD,![]() .E,F 分别是线段 SC,AB 上的一点,
.E,F 分别是线段 SC,AB 上的一点, ![]() .
.
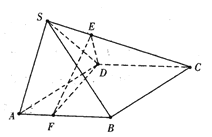
(1)求证:![]() 平面SAD;
平面SAD;
(2)求平面DEF与平面SBC所成锐二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com